We wanted to find the weight per cm3. In systems of equations with many variables and equations, we should start with a matrix. In the matrix below we have rows by A, B, C (%), W (g/cm3).We can reach the identity matrix with 3 row operations. First, R1 : (-43/584)R1 + (275/1168)R2 – (35/584)R3. Second, we do R2 : (7/43)R1 + (1/430)R2 – (3/215)R3. And R3 : -4R1 – 15R2 + (1/6)R3 finishes it off. Then, we can find that the mixture has 40 g/cm3. Finally, finding the 1:2:3 ratio is easy because in both powder 1 and the mystery mixture, A=B. Powder 2 : powder 3 must equal 11:3, making the ratio of A:B:C is 67:67:36. To get A:B:C to equivalent 2:2:3, we must add 129 1’s to the 1:2:3 ratio to get 129:11:3, we have A:B:C equals 196:196:294, or 2:2:3. Our answers are 129:11:3 and 35.86 g/cm3.
\left(\begin{matrix} 25 & 25 & 50 & 35 \\ 50 & 20 & 30 & 44 \\ 20 & 75 & 05 & 43 \end{matrix}\right) \overrightarrow{_{-\frac{43}{584}R_1+\frac{275}{1168}R_2-\frac{35}{584}R_3\rightarrow R_1}} \left(\begin{matrix} 1 & 0 & 0 & 0.6 \\ 50 & 20 & 20 & 44 \\ 20 & 75 & 05 & 43 \end{matrix}\right) \\[16pt] \left(\begin{matrix} 1 & 0 & 0 & 0.6 \\ 50 & 20 & 20 & 44 \\ 20 & 75 & 05 & 43 \end{matrix}\right) \overrightarrow{_{\frac{7}{43}R_1+\frac{1}{430}R_2-\frac{3}{215}R_3\rightarrow R_2}} \left(\begin{matrix} 1 & 0 & 0 & 0.6 \\ 0 & 1 & 0 & 0.4 \\ 20 & 75 & 05 & 43 \end{matrix}\right) \\[16pt] \left(\begin{matrix} 1 & 0 & 0 & 0.6 \\ 0 & 1 & 0 & 0.4 \\ 20 & 75 & 05 & 43 \end{matrix}\right) \overrightarrow{_{-4R_1-15R_2+\frac{1}{6}R_3\rightarrow R_3}} \left(\begin{matrix} 1 & 0 & 0 & 0.6 \\ 0 & 1 & 0 & 0.4 \\ 0 & 0 & 1 & 0.2 \end{matrix}\right)Tag: solution
Solution to Mixing Glasses
We wanted to find the minimum number of mixes to equally distribute liquid A. It is critical to note that liquid B’s positions do not matter. There are many ways to do this in the minimum mixes, but they are essentially the same. First, mix the glass with 500mL of liquid A with another. We now have 2 glasses with 50mL and 1 with 150mL. Mix one of each. Finally mix both glasses that now have 100mL of liquid A with the 2 that have none. And there we have it. It takes 4 mixes to get 50mL of liquid A in each of the 5 glasses.
Solution to Crazy Connections
We wanted to find the minimum number of points of each colour for a set. The most important thing to notice is that if one type of point connects to another type at a different frequency than vice versa, than the ratio of their sizes is the inverse of that difference. Put simply, if red points connect to 2 orange points and each orange point connects to 1 red point, there are twice as many orange points as red points. Repeat this to find a collective ratio of 1:2:4:3:1:1. Since red points connect to 1 other red point, we can thus find our answer. There is a minimum of 2 red points, 4 orange points, 8 yellow points, 6 green points, 2 blue points, and lastly, 2 purple points.
Solution to Opposite Lines
In this challenge, we wanted to find the antiderivative of f(x), given the above, and that the derivative of h(x) is 0.5. First, lets find f(x) in terms of h(x).
f(x)=-1/h(x)Then we can find the derivative of f(x) to be -2. The antiderivative of this, f(x), is -2x+c. The antiderivative of f(x), therefore, is -x^2+cx+c
-x^2+cx+cSolution to Surprising Non-Congruency
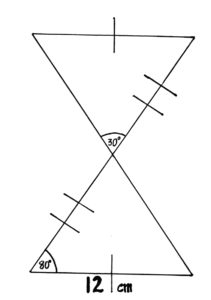
We wanted to find the length of the side which is comprised of the non-shared sides. The first thing we need to note is that, as stated in the problem, the angle opposite 30° is also 30°. We will later be able to use the law of sines to solve for the lower length. As for the angle opposite the 80°, it has to be exactly 100°. We know this because there are exactly 2 possible triangles, as mentioned in the problem, and we have both. And we can use the sine law again to find the length of the side opposite the newly-proven 100° angle. Doing this will allow us to get the answer, approximately 47.27cm.
Solution to Choosing Connections
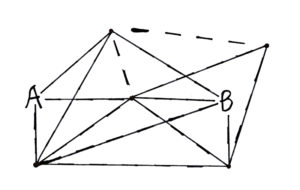
In this challenge, we wanted to find the maximum number of connections that we could add within the given conditions. Those conditions were only connecting on dotted lines, and exactly on path from A to B that goes through all other points. Note that there may be other paths from A to B, but those may not go through every point. The first step to solving this is to consider the points on the right. If we end with them, then we must come from the upper one. Then we can go to the lower. That’s because the upper one cannot reach B. If we do this, we can have an extra connection between the lower points. That one connection is needed to reach the maximum. The rest follows quickly. We are coming through the middle, so the left points must connect. We have to include the right points, so the others can all connect to B. At this point, we must remove as few outer connections as possible on the left. That would be 1, from the upper left to the centre. Now we have our final answer: 13 connections!
Solution to Parallel Pentagon
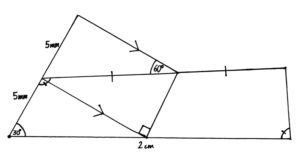
We are trying to find the area of the Pentagon this time. The first thing we can do is use the Transversal Parallel Line theorem to find that the left angle in the central triangle. Knowing that it must be 60°, we can find that the angle on the right must be 30°. We know this because the sum of the angles in a triangle is 180°. Then we can use these 2 theorems a bit more to show that all three triangles are equal. We do need to use strait angle = 180° too in some methods. Then we continue the upper parallel line to divide the pentagon into 5 triangles. We can then prove that the new ones are 30° 60° 90° too. And then all that’s left is the pythagorean theorem and area of a triangle. After all this, we have our answer: 5*(5mm * 5√3 mm / 2) = 312.5√3 mm2.
Solution to Equation System
This time, we wanted to find the solution to this system of equations. The simplest way to do this is by using the first equation to find a in terms of b, and then substitute in the second equation. We will find that a=-b-3, and so…
-3b-b^2+3 = -b-3-74.We will find that this solves to the quadratic b^2+2b-80=0, which is equivalent to (b+10)(b-8)=0, and so has solutions b=-10 and b=8. Plug this in to our equation for a in terms of b and our solutions are as follows:
solutions: a=7,b=-10;a=-11, b=8Solution to Adjacent Triangles
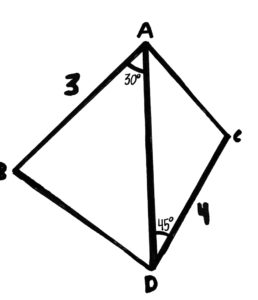
This time, we wanted to find the area of the left triangle on the left, given that the area of the one on the right has area √2. First, let’s remember that the area of any triangle, say △xyz, has area xy*yz*sin(∠xyz)*0.5. Now, we can use this formula’s inverse to find the length of ad, which will be 1. And then, we can use this to find the area of △abd, which is 0.75. ∴ the area of △abd is 0.75.
Solution to Path Counting
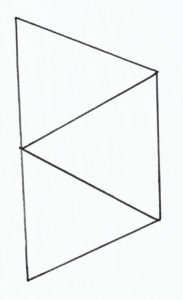
In this challenge, we wanted to find the number of paths. The easiest way to do this is by labeling the intersections, and noting the paths by the intersections. That’s because all paths start and end at intersections, and never enter the same one twice, so the paths are defined by the intersections. Now, this can be organized in anyway, like from fewest intersections to least, and then alphabetical order, or whatever. The important thing is that you dont miss any paths. Then you should get a total of 46 paths. And that’s our answer: there are 46 paths.
