Tag: solution

Solution to Kayoed Kangaroo

Kangaroo chasing Sheep

Kangaroo was bumped by Sheep. Now Kangaroo is angry, and the chase is on: can Sheep escape? No. Of course not.

Sheep runs 10 meters away in a single second, but Kangaroo is not worried. Kangaroo jumps directly toward Sheep, but is still 1 meter out of range. But no matter where Sheep runs, Kangaroo will jump behind, so that Sheep is just over 6.5 meters away. Sheep is forced to run directly toward the pond.

Perhaps, if Kangaroo were not quite so fast, Sheep could have escaped. Sometime later, perhaps we will discuss a scenario where Kangaroo jumps only thrice per second, and Sheep flees at 9 meters per second.

Solution to Curt Cutting

From a deck of n cards, we cut—randomly select with replacement—10 different cards before cutting a card we had seen before. We are trying to determine the probability of achieving this result for n from 10, the lowest n for which result is possible, up to n < 30.

{10\over10}\cdot{9\over10}\cdot{8\over10}\cdot{7\over10}\cdot{6\over10}\cdot{5\over10}\cdot{4\over10}\cdot{3\over10}\cdot{2\over10}\cdot{1\over10} \cdot{10\over10}\ =\ {9!\,10\over10^{10}}\\[16pt] \operatorname P n \propto {(n-1)!\,10\over (n-10)!\,n^{10}}
Probability distribution of n

For n = 10, the calculation is simple and shown above. For n = 11, is the calculation more complex? No: 10!9/1110 works! However… this does not work for n = 12. 11 * 10 … 2 does not match the equation used above to derive the formula. It should be 11 * 10 * … 3, of course. With that error avoided, the formula above is produced, and this can easily produce a probability distribution. The expected value of n is then easily calculated to be ≈23.31.

Solution to Cantankerous Circle

We’re trying to determine the average distance from a random point in a circle to the centre, for various definitions of average. The simplest, the arithmetic mean distance, is ≈ .6667.

\iint_R \ln \operatorname f x\ \delta A

First, the geometric mean. The basic integral required to solve this is above. It’s not a very hard integral, especially for a circle. It’s equal to 2π times the integral from 0 to 1 of x2 ln x. That’s a relatively simple integration by parts, which many already know how to do–but for completion:

\int_0^1 x^2 \ln x\ \delta x \\[16pt] \int_0^1 \ln x \cdot x^2\ \delta x \implies \xcancel{\left[ {x^3\ln x\over 3}\right]}_0^1-\int_0^1 \frac{x^2}3 \delta x \\[16pt] = {\left[\frac{x^3}9\right]}_0^1 = -\frac19

Substituting, the geometric mean distance is e-2/9 ≈ .8007. Note that this is -2/9 not -1/9 because we multiplied the integral by 2π.

Second: the quadratic mean. Since we’re using the identity function, this is a rather easy one. The integral of x2 times x is 1/4 x4, from 0 to 1 that’s just 1/4. We take the square root of 1/8, not 1/4, for the same reason as with the geometric mean. Thus, the quadratic mean distance is ≈ .3536.

Third: the harmonic mean. We saved the best for last: the determinant of the transformation from cartesian to polar coordinates is x. 1/x times x is 1. It’s the easiest integral of all! The harmonic mean distance is .5.

And last, the extra easy cool-down problem, that’s not even really integration at all. This one is fairly obvious: the median distance is ≈ .7071.

Solution to Spry Springs

We’re trying to determine the characteristics produced by combining multiple springs together in a row. It seems that all the springs should experience the same horse. When a spring is under some amount of compression, if it is not changing in length, it must be exerting an equal outward horse. To simplify, assume the combined spring is not moving. Obviously, a spring moving about will not change its characteristics–unless it is accelerating. So, when a spring has 5 newtons of horse on its left, it also has 5 newtons on its left, and we consider it to be under 5 newtons of compressive horse. Since one spring’s left is on another’s left; they are in a line. The nominal length is the length when a spring is under no horse. When the combined spring is under no horse, all springs inside are also under no horse, and thus the combined spring has a nominal length equal to the sum of the nominal lengths of the component springs. The spring constants may seem a bit more complex, because the horses remain the same, not the displacements. But really, this just means we summate the inverses. So 1 metre per Newton, plus 50 centimetres per Newton, equals 1.5 metres per Newton.

Spring ConstantsNominal lengths
1.42N/m3m
1.091N/m8m
.6154N/m8m
.25N/m15m

Solution to Macrocephalous Measurement

The mechanism measuring the capacity of the large container.

We’re trying to find the volume of the container on the left. First, there is a need to create a system of equations representing the volumes. The linked cylinders will be filled with fluid, to neglect their volume. Let the volume of the measured container be V1, the auxiliary container, V2. Let their pressures be P1 and P2. The atmospheric pressure will be P0. The volume pushed, and remaining volume in the main and auxiliary containers: α, β, and γ respectively. The shift of the cylinder is Δ(γ). Using the fact that pressure times volume is constant for constant temperature, we end up with the following system of equations:

V_1 \cdot P_1 = \alpha \cdot P_0 \\[8pt] V_2 \cdot P_2 = \beta \cdot P_0 \\[8pt] P_1 + P_2 = 2 P_0 \\[8pt] \operatorname \Delta \gamma = \gamma + \alpha – V_1 = \beta – V_2

We know that Δ(50mL) = 30mL in the case given, but for a full solution, a general formula will be given here. But in the general case, the known variables are γ and Δ(γ). The third equation provides the first step: divide both sides of it by P0. This is because the value of atmospheric pressure is not relevant, only the ratios to it! We also divide the first and second equations by P0 to complete the switch, removing the irrelevant variable to enable completion of the problem. You may ask why this variable was included in the solution: for completeness; to demonstrate that it’s unimportant. Next: split the fourth equation as shown below. This easily resolves, separating the volumes from the variables. Note that V1 = α + Δ(γ) – γ, so removing it at present is no problem–it can easily be found later.

\alpha = V_1\cdot{P_1 \over P_0} = V_1+\operatorname\Delta\gamma-\gamma \\[8pt] \beta = V_2\cdot{P_2 \over P_0} = V_2+\operatorname\Delta\gamma \phantom{-\gamma}\\[16pt] \alpha-\alpha\cdot{P_1 \over P_0}+\operatorname\Delta\gamma = \gamma \\[8pt] \beta -\beta \cdot{P_2 \over P_0}\phantom{+\operatorname\Delta\gamma} = \gamma

Combining the last two equations, it becomes easy to find the one in terms of the other. The equation below describes the simplified relationship without knowing the volume of the auxiliary container. Know that V2 = β + Δ(γ), and as we know that V2 = .5L, so β = .5L – Δ(γ). To solve for this specific case–for to only solve generally and not in the specific case would be just as incomplete as would the opposite–we then fill in our known values of Δ(γ) = 30mL, γ = 50mL, and extending to β = 470mL. We get the value of α = (470mL/30mL – 2)(20mL) ≈ 27.33mL. Remembering from before that V1 = α + Δ(γ) – γ: V1 = ≈27.33mL – 20mL ≈ 7.333mL. The answer is then ≈7.333mL for the specific case and the equation below for the general case.

\alpha = \left(\frac\beta{\operatorname\Delta\gamma}-2\right)\cdot \left(\gamma-\operatorname\Delta\gamma\right)

Solution to Interlinear Interval

We are attempting to find the average number of steps in a certain mathematical game. Let us define a function which represents the average number of steps to completion. We will have this function be called T, for time, and have T(x) be the expected number of remaining steps at the position x. A review of the formal rules of the game and the definition of this function:

n \in \mathbb{N} \\[4pt] \operatorname f : \mathbb R, \mathbb Q \to \mathbb Q \\[8pt] \operatorname f {(p, x)} = \begin{cases} p > x : x-\frac1{2n} \\[4pt] p < x : x+\frac1{2n} \\[4pt] p = x : x \end{cases} \\[48pt] \operatorname T: \mathbb Q \to \mathbb N \\[4pt] \operatorname T(0) = \operatorname T(1) = 0 \\[12pt] \operatorname T(x) = x\operatorname T\left(x-\frac1{2n}\right)\ + \ (1-x)\operatorname T\left(x+\frac1{2n}\right)\ +\ 1

We can rephrase this equation to express T(x+1/2n) – T(x) in terms of T(x) – T(x-1/2n), a much more use-full equation. Consider a T(-1/2n). This extends the space of T beyond that which actually represents f–allowing us to find T(1/2n). T(-1/2n) = -1, so T(0) – T(-1/2n) = 1. Using the equation below: T(1/2n) – T(0) is 2n/(2n-1) + 1/(2n-1) = (2n+1)/(2n-1). This may then be extended further: T(1/n) – T(1/2n) is (2n(2n-1) + 2(2n-0) + 2) / (2n-2)(2n-1). Can we go for a formula in pi and sigma notation: yes. What about a polynomial formula, or at least something less hard to calculate? NO.

\operatorname T(x)-\operatorname T\left(x-\frac1{2n}\right)\ =\ \frac1{1-x} \ +\ \frac x{1-x}\left(\operatorname T\left(x+\frac1{2n}\right) – \operatorname T(x)\right)\\[24pt] \operatorname T(x) – \operatorname T\left(x-\frac1{2n}\right)\ =\ \left((2nx)!+\sum_{k=0}^{2nx}{(2nx)!(2n-k)\over k!}\right)\div \left(\prod_{l=1}^{2nx}2n-l\right)

And finally, we can summate T(k/2n) – T((k-1)/2n) for all k from 1 to n. The answer is, therefore, the following huge formula!

\Large {\Huge\sum_{k=1}^n}\left((2nk)!+\sum_{l=0}^{2nk}{(2nk)!(2n-l)\over l!}\right) \div\left(\prod_{m=1}^{2nk}2n-m\right)

Solution to Garbled Games

This challenge was to find the optimal strategy for player 5 of a certain game. This must be solved with probability density. Let the PDF before the guess of player n be fn, and that player’s best guess, x0. The derivative of the expected value must be zero, which can be simplified to:

x_0 \operatorname{f_n}x_0 = \int_0^{x_0}\operatorname{f_n}x \delta x

Solving for player 1, we get 3x0 = 2, and so x0 = 3/2. Using a the same process for players two through 5, we can find the answer. Shown is a table of the best guess, chance of victory, and expected value for players one two five, as well as the probability density function for the weight of the prize before each guess. The answer is thus a guess of exactly 0.1 kilograms, and you will win it exactly half the time.

\begin{array}{|r|rcl|} \hline \\ \text{Player} & \text{Guess} & \operatorname P {win} & \text{Value} \\[4pt] \hline \\ 1 & 3\over2 & 3\over4 & 9\over8 \\[4pt] 2 & 1 & 1\over2 & 1\over2 \\[4pt] 3 & 1\over3 & 1\over2 & 1\over6 \\[4pt] 4 & 5\over24 & 23\over48 & \approx.1 \\[4pt] 5 & 1\over10 & 1\over2 & 1\over20 \\[4pt] \hline \end{array}
  • Player 1
  • Player 2
  • Player 3
  • Player 4
  • Player 5

Solution to Scrupulist Square

Example setup

The challenge we are solving is about a graph derived from random points. The probability of connection between two is equal to 1 minus their distance, implying that each node has a loop. A node is chosen randomly, then a node is chosen of the odes connected to it, including itself. To find the probability that the second node has more connections than the first, We would need to determine the average number of connections to a given node. Since distance is best averaged in polar coordinates, this is a bit tricky. The trick is to divide the square into eight triangles, and use the secant function. The full process of integration is shown below. Now, Consider 2 points in a square. Consider the perpendicular bisector of the line segment connecting them. The square is divided into two parts, and on either side, one of the points is always closer. For the infinite case, the point with greater area will have more connections. Since the point at which it is exactly evenly cut must always pass through the square’s centre, any two points with equal distance from it will split the square evenly. So, for the infinite case, we may simplify to the probability of choosing a point closer to the centre. So for a given point, take the area of this circle, and divide by the total average fraction of all points it connects to. Given that, for lesser n, a point is always connected to itself, this amount needs to be adjusted. Specifically, with n points and a given point connecting to x fraction of an infinite selection, the actual fraction is x*(n-1)/n + 1/n. Instead of integrating over this circle, take the volume of an elongated slanted cone, which is equivalent. Let the point be a distance r from the cenre. The peak is always at the point, with height 1. The lowest point is 1 – 2r. Below is the calculation for the area of the shape. What is its average volume? Integrating again in polar coordinates, we get approximately .877! This is a messy integral and does not need to be fully shown. And lastly, the

\text{Finding the average distance to the corner of a right triangle,} \\ \text{with adjacent side }a\text{ and angle }\theta\text . \\[16pt] \int_0^\theta \int_0^{a \cdot\sec \theta} r^2 \delta r \delta \theta \\[12pt] =\int_0^\theta {{(a \cdot\sec \theta)}^3\over3} \delta \theta \\[12pt] ={a^3\over3} \cdot \frac12 \cdot {\left( \sec\theta\cdot\tan\theta+\log{\left(\cos\frac\theta2+\sin\frac\theta2\right)} – \log{\left(\cos\frac \theta2 – \sin\frac \theta2\right)}\right)} \\[12pt] = \operatorname f{(a, \theta)} \\[12pt] \operatorname g{(x, y)} = \\[8pt] \operatorname f{\left(x, \arctan\frac yx\right)} + \\[4pt] \operatorname f{\left(y, \arctan\frac xy\right)} + \\[4pt] \operatorname f{\left(x, \arctan\frac {\frac1{\sqrt2}-y}x\right)} + \\[4pt] \operatorname f{\left(x, \arctan\frac {\frac1{\sqrt2}-y}x\right)} + \\[4pt] \operatorname f{\left(\frac1{\sqrt2}-x, \arctan\frac y{\frac1{\sqrt2}-x}\right)} + \\[4pt] \operatorname f{\left(\frac1{\sqrt2}-y, \arctan\frac x{\frac1{\sqrt2}-y}\right)} + \\[4pt] \operatorname f{\left(\frac1{\sqrt2}-x, \arctan\frac {\frac1{\sqrt2}-y}{\frac1{\sqrt2}-x}\right)} + \\[4pt] \operatorname f{\left(\frac1{\sqrt2}-y, \arctan\frac {\frac1{\sqrt2}-x}{\frac1{\sqrt2}-y}\right)} + \\[4pt] \\[32pt] \text{Elongated cone, radius r, height 1, and height of cone 2r.} \\[16pt] A = \pi r^2 (1-2r) + \frac13 \pi r^2 (2r) \\[8pt] = \pi r^2 – \frac43 \pi r^3 \\[32pt] \text{This volume, integrated in polar coordinates.} \\[16pt] {\Large8\int_{-\frac\pi8}^\frac\pi8 \int_0^{a \cdot\sec\theta}} {\pi r^2 – \frac43 \pi r^3 \over{n-1\over n}\operatorname g{( \frac1{2\sqrt2}+r\cos\theta, \frac1{2\sqrt2}+r\sin\theta)}+\frac1n} {\Large \delta r \delta \theta = } \left({5\pi\over36}- {\tanh^{-1} {\sqrt2-1}\over 16\sqrt2}\right) \frac n{n+1} – \frac1n \\[12pt] \boxed{\huge\approx.877} \\[12pt] \text{8 because there are 4 triangles, and to get average, divide by area .5.}

Solution to Preposterous Primes

This challenge was the last before an extended summer break. We left off unsure whether or not a sequence reached infinity at a finite point. Well, it does, and almost certainly at 23. But why? The solution is below.

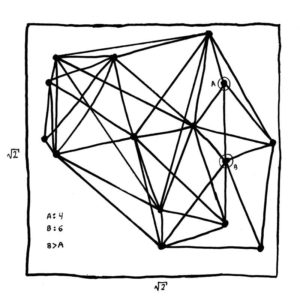
Let us arrange the set of natural numbers into a sequence T. T begins with 1. For any Tn, Tn+1 is the lowest number prime connected to n that is not in the sequence T. If there exists none, then look to Tn-1, and repeat this process. If there are no more prime numbers connected to any previous numbers, then continue with the lowest natural number not yet in the set.

Within these constraints, a is always maximized, and n minimized for the value of a. This sequence is then: 1, 2, 4, 3, 6, …, 23. Now, what happens if this set is infinite? Well, some numbers would be skipped. Specifically, any dead end of connections not immediately followed would never be. This sequence is actually the best way to compute these sets. But computing to a high amount isn’t proof. But this is still helpful.

In order for there to be no infinite sets, there must be an infinite amount of finite sets. For each prime or the form 6n±1, or all those greater than 3, there are at least 3 numbers in its set. For 6n+1, they are 6n+1, 12n+2, and 12n. For 6n-1, they are 6n-1, 12n-2, and 12n-4. When n is even, both extend to 12n-3 and 12n-6. This proves that twin primes like 11 and 13, but not necessarily 17 and 19, must connect. This matches experimentation. Consider, in this sequence, that 2, 3, 5, 7, 9, 11, 17, 19, and 23 all are the first of their sets. Is 9 special? Yes, for any prime multiple of 3, only 1 number is connected to it, which is below. But 9 is alone, and so can start, and end, its set. But since there is no infinite occurrence of this, then there must be an infinite number of disconnected primes. This is impossible.

The reason for this, at last, is simple: an infinite number of sets that have a prime lowest number may not leave any composite spaces. That’s where the sequence comes in: since the first element the lowest and prime, a prime’s set must cover each number up to the next prime. But it must also contain those 2 additional numbers mentioned earlier. The next set must be unable to reach those, but able to reach all others. Here probability does the trick: as one goes through primes, the probability of this dwindles on the order below. Since this does not approach infinity, the weak law of large numbers tells us there must be an infinite set, and since 23’s grows so much so quickly, it is almost certainly the answer. Though there is a tiny probability of otherwise, and there could be a great number of very large sets afterwards, there must be a large one eventually, if not immediately.

\operatorname \mathcal 0 {\left({n\over{2\choose{\frac n{\ln n}}}\ln n}\right)}

Thus concludes Preposterous Primes, and zacharycormack.net‘s extended summer break.

Solution to Fascinating Frequencies BONUS

\text{let }x,\,y,\,z\in\R,\;x\leq y\leq z\\[8pt] \text{if }\;\exists!\;\{x,\,y,\,z\}: \operatorname fa=\operatorname gb=\operatorname hc\;\; \forall\;\;\{a,\,b,\,c\}\equiv\{x,\,y,\,z\},\\[4pt] \text{then }\;f\bigcirc g\bigcirc h\\[8pt] \text{if }\ f\bigcirc g\bigcirc h\;\ \text{and }\ f’\circledcirc g’\circledcirc h’,\ \;\text{then}\;f\circledcirc g\circledcirc h

We’re trying to find a set of three functions that satisfied a certain property. Look closely at it, and you see that what it really means is that, firstly, all three lines are concurrent at exactly three points. Then, their derivatives have the same property. This is recursive. Consider that the derivative of a sine wave is also a sine wave. We then have a relatively simple solution to the problem, but which is tricky to figure out.

\left. \begin{array}{l} \text{if $0\le x\lt3\pi$:} & \sin x \\ \text{if $x\ge3\pi$:} & f(-x) \\ \text{if $x\lt0$:} & e^x \\ \end{array} \right\} =f(x) \\[8pt] g(x) = -f(x)\\[8pt] h(x) = 0\\[16pt] f\circledcirc g\circledcirc h