You will need to understand calculus and linear algebra to solve this problem.
f(x) = g(x+1)-x,\space g(x) = f(2x)-2Today’s challenge is this: what is the derivative of f( g(x) )? Good luck!
Tag: problem
Altitude Triangle
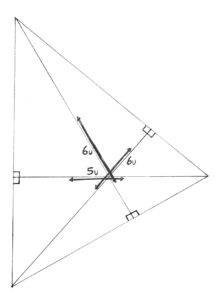
Todays challenge requires you to understand the pythagorean theorem, in the topic of geometry. You will also need to comprehend angle theorems.
The altitudes in a triangle measure 5, 6, and 6 units. The perimeter of said triangle is 20 units. The challenge for today is: What’s the area?
Perfect Square
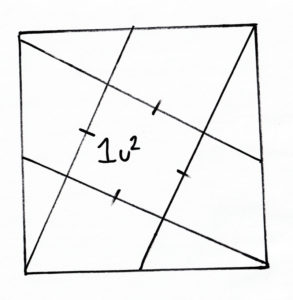
You will need to understand algebra and angle theorems to do today’s challenge.
With today’s challenge, we’ll be trying to find the area of a square! All outer regions of this square have equal area, and the inner region, a square itself, has side length 1. Can you find the area of the big square? Good luck!
Divided Rectangle
You will need algebra and geometry to solve today’s challenge.
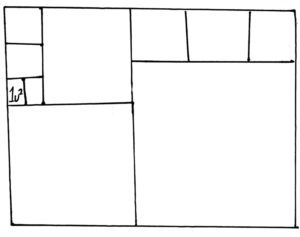
Can you find the area of the large rectangle that encompasses all the squares, thereby solving today’s challenge? Good luck!
Shaded Square
In today’s challenge, you will need the concepts of geometry and trigonometry.
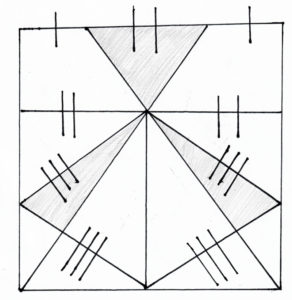
For today’s challenge, you must find the area of the non-shaded portion of the large square. The square has an area of 1 square unit.
Optimal Route
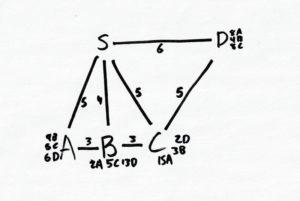
Today’s challenge covers the concept of optimal path-making.
Can you find the bus route that is the best for everyone? The bus driver counts too. Each big letter is a bus stop. The small letters next to the big letters represent other stops that people at the station want to go to. The numbers are the amount of people going to that stop. S it the bus depot, the start and end.
Maximum Seperation
This challenge utilizes the concepts of basic graph theory and counting.
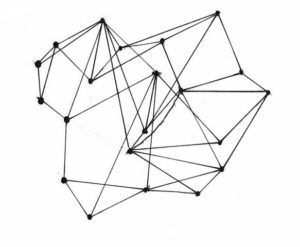
The challenge is to find the highest possible minimum number of lines needed to be traversed to get between any 2 arbitrary points.