Tag: problem

Devising Deactivation

To solve this challenge, you will need to use geometry, trigonometry, and algebra, to do pathmaking.

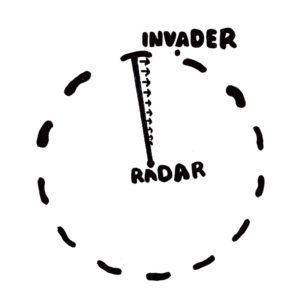
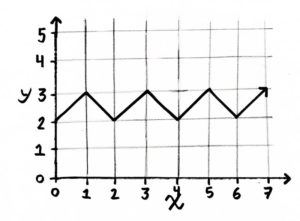
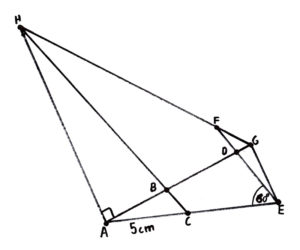
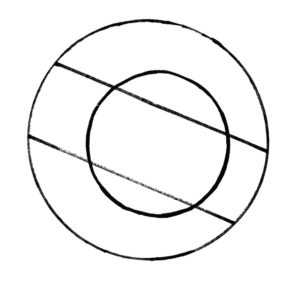
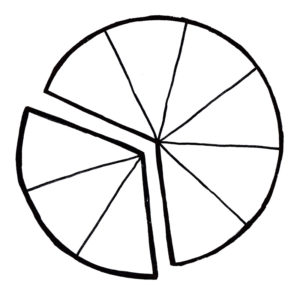
Map of the radar that must be deactivated.

You are working for the government as a mathematician and they tell you of a problem. There is a plan afoot to compromise an enemy radar station. It is critical that the invading crew member is undedected, as the enemy must not know that their radar is sending them misinformation. However, the radar has a range of 100 metres and completes a rotation every 12 seconds. The fastest crew member can only sprint at 7 metres per second with their toolkit. Because of the radar’s length and rotation speed, it is nearly impossible to disable it undetected. None of the simple strategies work. The challenge is to find a path that the invader can take without being detected.

Solution

Absurd Algebra

Extreme algebra knowledge and skills are required to solve this challenge.

Absurd Algebraic Graph.

This time, we are faced with a strange graph. When x rounds down to an even number, the slope is 1. But when it rounds down to an odd number, the slope is -1. This makes an intriguing zig-zag pattern with peaks always at 2 or 3. But what equation could possibly give such a line? Well, that is the challenge.

Solution

Crazy Quadrilateral

You will need to use geometry, angle theorems, trigonometry, and your brain to solve this challenge.

Crazy Quadrilateral

We begin with a quadrilateral AEGH. We then draw a line from A to G to make ΔAEG and ΔAGH. ΔAEG is an isoscelese triangle. Next, we draw a line from point E to a new point, F, such that ∠AEF measures 60°. This makes a new point, D, where AG intersects FE. After that, we draw a line HC so that it is parallel to FE and intersects AG at point C. This makes ΔABC ~ ΔADE ~ ΔHAG. The challenge is to find ∠FEG if ∠HAG measures 90°.

Solution

Captivating Circles 6

This is the final Captivating Circles challenge, this challenge requires the concepts of geometry and trigonometry.

Captivating Circle #6

We begin this challenge with 2 concentric circles. The smaller circle divides the larger 1 into 2 equal pieces. We then draw 2 parallel chords in the large circle, which divide it evenly into three. They do not divide the small circle into three equal pieces. The challenge is then to find the area of the biggest piece in the smallest circle if the large circle has radius 1.

Solution

Captivating Circles 3

In this captivating circles challenge, you will need to use some algebra, some combinatorics, and some serious brainpower.

Captivating Circle #3

For our newest captivating circle, we are dealing with splitting oranges. The orange starts with N slices in a circle. It is then divided into 2 rings with A slices and B slices. In the diagram, N=9, A=3, and B=6. We then count one 3 and one 6. One of these rings is splitted to make 3 rings in all. We then count these rings. This continues until we can no longer split any rings as they all contain 1 slice. It happens that at the end, the number 1 is counted at least 3 more times than 2, which is counted at least 3 more times than 3, etcetera until the largest number counted. The challenge is this: what is the maximum value for N?

Solution

Captivating Circles 2

Today, we have a new captivating circle, and it is the first challenge to require the use of combinatorics. It also requires some trig and pathmaking.

Captivating Circle #2

Our second captivating circle is a circle with 7 points on its circumference. The points are equally spaced. Each point connects to 2 others through the circle and 2 others through a straight line. No points can connect to another through both a line and arc. The circle has circumference π. How many possible different sets of connections can be made? And of these, what is the highest possible distance that must be traversed to get between 2 points?

Solution

Captivating Circles 1

Today we begin a special series, captivating circles. This challenge requires trigonometry and geometry.

Captivating Circle #1

The first captivating circles challenge is to find the area of the shaded region in the circle in the diagram. All vertices of the white triangle are on the circumference of the big circle, and the small circle is tangent to all 3 sides of the triangle. You may find that this problem requires theorems and formula’s not normally required. Do not be afraid to research the tools you need to solve this problem or other captivating circles, it’s knowing which tools to use that’s the challenge.

Solution

Mystery Mixture

Today’s challenge requires matrices.

A mixture is made by mixing 3 powders: powders 1, 2, and 3. The powders are each made from different amounts of the same 3 ingredients. The ingredients are named A, B, and C. Powder ratio’s are A : B : C. Powder 1 is 1 : 1 : 2 and weighs 35 g/cm3, powder 2 is 5 : 2 : 3 and weighs 44 g/cm3, and powder 3 is 4 : 15 : 1 and weighs 43 g/cm3. The mystery mixture is 2 : 2 : 3. The challenge is: how much of each powder is in the mixture, and how much does the mixture weigh per cm3? Answer in 1 : 2 : 3 and g/cm3.

Solution

Mixing Glasses

Today’s challenge requires the concept of Algebra.

5 glasses contain amounts of various liquids. The glasses are numbered 1 to 5. Non-prime glasses contain liquid A, and prime glasses contain liquid B. Odd glasses contain 750mL, and even ones contain 500mL. When you mix 2 glasses they then contain the same quantity of liquid in the same proportions. The challenge is to find the minimum number of mixes to ensure that each glass contains the same quantity of liquid A.

Solution