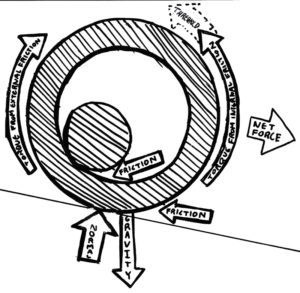
We’re trying to find the rate at which a cylinder rolls. This is actually rather simpler than you would think. For every metre the small cylinder rolls, the big one rolls three. The small one has internal friction with the big one. But, this is more than that of the big one and ground! The push of this friction is not only exerted by the big cylinder onto the small, but vice versa! Now, the cylinder would roll because of the counterclockwise torque applied by the friction with the ground. But the internal friction is so much stronger that it overpowers that torque with an even stronger clockwise torque threshold. Remember, it only happens when the counterclockwise torque is applied, so it is only a threshold. It will not cause the cylinder to roll backwards or anything crazy like that. This principle also applies to the normal force exerted by the large cylinder unto the small. Because of this, it is as if the small cylinder did not exist! Well, not really. But in a purely mathematical concept, it will be once equilibrium is reached. Knowing this, we need only look at the big cylinder. The acceleration gravity applies downward, combined with the normal force from the ground, exerts a total force dictated by the equation below. For 9.807 m/s2 and 15°, it gives 9.473 m/s2. Per metre, the kinetic friction is 1 kg/s. To equal the acceleration downwards, we divide, and get 9.473 metres per second.
\vec F_g-\vec F_n=F_g\cos\theta\\[4pt] =9.807\frac m{s^2}\times0.9659\\[4pt] =9.473\frac m{s^2}