Challenges cover a variety of topics
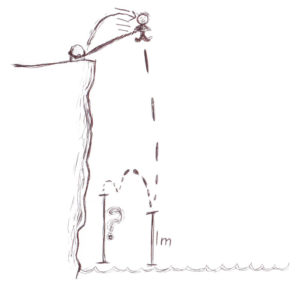
This challenge has calculus and algebra.
We begin this problem by defining a few variables and functions, see below.
Let a ‘functional triangle’ be a relationship between three functions shown, denoted by the two large circles.
The properties of such are shown.
Then, a ‘meta-functional triangle’ is denoted in the same manner be a functional triangle with the given additional property.
The challenge is to find a meta-functional triangle. Good luck!
For our final Fascinating Frequencies challenge, we will be using chemistry, physics, simulations, and orbits.
An experiment is held in space station orbiting earth from a geostationary orbit. Unfortunately, the scientists onboard forgot to properly secure one side of the space station. The side pointing prograde. Well, at least not retrograde, but their orbit is still messed up seriously. The reaction was between sodium and fluorine, with 19 kilograms fluorine and 23 kilograms sodium. The mass of the space station is 500 megagrams, including remaining fuel. How many grams of fuel must the scientists burn minimum to bring their rocket back to geostationary orbit? The scientists’ rocket fuses hydrogen and oxygen.
You will need to use physics for this Fascinating Frequencies challenge.
An interesting device can be created when you have a wheel of gears. Of course, this wheel will have an even number of gears. If the device is anchored and you spin one gear, the others will all also spin at the same frequencies. But if you anchor the gear you spin, the others can spin around it. Try building this device yourself, it’s very cool. Say you make one of these devices with six gears. The radius of each gear is 10 centimetres, and the centripetal force felt by the gear opposite to the anchored one you are spinning is 1 metre per second squared. The challenge is to find what frequency the gear is spinning.
A physics simulation is needed to solve this challenge.
Bob the Bungee jumper from Baffling Bungee is upset about his bungee jumping experience. If you attempt the problem, you will soon see that Bob’s bungee jump will take too long. Far too long. This is because C5H8 is very springy. In fact, Bob’s bungee jump would take about 2 months … if you were thinking of a mathematical model. You see, the diagram shows a cliff behind Bob. The rubber is so springy he would bash into it, cutting his jump short. But set that problem aside for now. This challenge does not concern those. In bob’s jumps, the ups and downs would gradually, very gradually, become smaller and smaller. But they would still occur at the same frequency. Can you guess today’s challenge? Calculate that frequency.
Some chemistry principles are required to solve this challenge.
In this Fascinating Frequencies challenge, we will cover fluid dynamics. A perfect homogeneous sphere with radius 10 cm and mass 1 kg hits the middle of a pond of pure water on earth. It’s velocity is 1 m/s downward. The temperature of the pond is a uniform 20° celsius. The pond will begin to ripple. There are no animals in the pond to interfere with this. The challenge is to calculate the frequency of the ripples.
This challenge involves orbits.
A geostationary orbit is one where the satellite stays in the same position relative to the ground. This works because the earth spins; the velocity that keeps it over the same spot increases while the velocity needed to orbit decreases. At some point, they intersect. All geostationary orbits must be at the equator, and have the same altitude althroughout. If you wanted to get a satellite into geostationary orbit around a planet with mass of 5,000 yottagrams that completes 1 revolution every 20 hours, how fast would your orbital speed be at apoapsis? The apoapsis is the highest point in an orbit.
This challenge is the first of a new science challenge series, Fascinating Frequencies. You will need to use physics to solve this challenge.
Some radioactive particles are decaying. They are decaying in different ways, but each type of decay releases the same amount of energy. If the particle undergoes beta decay, it will release an electron and positron, both traveling at half the speed of light in a vacuum. If it undergoes gamma decay, it will release a photon. The challenge is to find the frequency of this photon.