Challenges cover a variety of topics
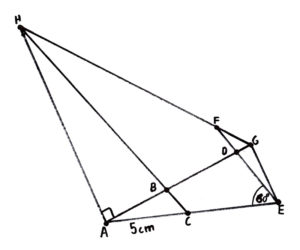
Extreme algebra knowledge and skills are required to solve this challenge.
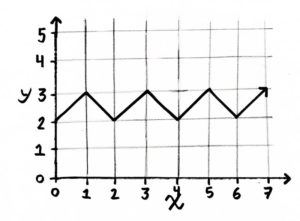
This time, we are faced with a strange graph. When x rounds down to an even number, the slope is 1. But when it rounds down to an odd number, the slope is -1. This makes an intriguing zig-zag pattern with peaks always at 2 or 3. But what equation could possibly give such a line? Well, that is the challenge.
You will need to use geometry, angle theorems, trigonometry, and your brain to solve this challenge.
We begin with a quadrilateral AEGH. We then draw a line from A to G to make ΔAEG and ΔAGH. ΔAEG is an isoscelese triangle. Next, we draw a line from point E to a new point, F, such that ∠AEF measures 60°. This makes a new point, D, where AG intersects FE. After that, we draw a line HC so that it is parallel to FE and intersects AG at point C. This makes ΔABC ~ ΔADE ~ ΔHAG. The challenge is to find ∠FEG if ∠HAG measures 90°.
This is the final Captivating Circles challenge, this challenge requires the concepts of geometry and trigonometry.
We begin this challenge with 2 concentric circles. The smaller circle divides the larger 1 into 2 equal pieces. We then draw 2 parallel chords in the large circle, which divide it evenly into three. They do not divide the small circle into three equal pieces. The challenge is then to find the area of the biggest piece in the smallest circle if the large circle has radius 1.
You will need to use algebra to solve this challenge. Some programming would be extremely useful as well.
In the video-game “Battle of the Blobs”*, a blob is a circular creature that deals damage over time proportional to its current area. A blob’s area will shrink proportionally to damage dealt to it. The damage over time is not dealt at short intervals, rather is always being dealt, but with the same rate. Our challenge begins when 2 blobs, Jack and Jill, battle each other. The radius of Jack is 1, and the radius of Jill is 1.5. Clearly, Jill will kill Jack. The question is what will be Jill’s radius after fighting Jack, assuming the only change in a blob’s size is caused by damage from the other.
*”Battle of the Blobs” is not a real video-game.
You will need all your skills in graph theory, and pathmaking, algebra and combinatorics to solve today’s challenge. Good luck!
This captivating circle has been divided in to many sections. By combining these sections, you can make many different composite shapes. The challenge is to see how many shapes you can make. This includes the entire circle.
In this captivating circles challenge, you will need to use some algebra, some combinatorics, and some serious brainpower.
For our newest captivating circle, we are dealing with splitting oranges. The orange starts with N slices in a circle. It is then divided into 2 rings with A slices and B slices. In the diagram, N=9, A=3, and B=6. We then count one 3 and one 6. One of these rings is splitted to make 3 rings in all. We then count these rings. This continues until we can no longer split any rings as they all contain 1 slice. It happens that at the end, the number 1 is counted at least 3 more times than 2, which is counted at least 3 more times than 3, etcetera until the largest number counted. The challenge is this: what is the maximum value for N?
Today, we have a new captivating circle, and it is the first challenge to require the use of combinatorics. It also requires some trig and pathmaking.
Our second captivating circle is a circle with 7 points on its circumference. The points are equally spaced. Each point connects to 2 others through the circle and 2 others through a straight line. No points can connect to another through both a line and arc. The circle has circumference π. How many possible different sets of connections can be made? And of these, what is the highest possible distance that must be traversed to get between 2 points?
Today we begin a special series, captivating circles. This challenge requires trigonometry and geometry.
The first captivating circles challenge is to find the area of the shaded region in the circle in the diagram. All vertices of the white triangle are on the circumference of the big circle, and the small circle is tangent to all 3 sides of the triangle. You may find that this problem requires theorems and formula’s not normally required. Do not be afraid to research the tools you need to solve this problem or other captivating circles, it’s knowing which tools to use that’s the challenge.
Today, we have a special challenge. To celebrate the changing of clocks, this challenge requires only use of time differences.
Joanna the scientist from Pure Water is now attempting to get her P.H.D by teleporting a muon from Vancouver to Toronto. The muon will arrive at Toronto at 2AM. When, in Vancouver time, did the muon depart?
Today’s challenge requires matrices.
A mixture is made by mixing 3 powders: powders 1, 2, and 3. The powders are each made from different amounts of the same 3 ingredients. The ingredients are named A, B, and C. Powder ratio’s are A : B : C. Powder 1 is 1 : 1 : 2 and weighs 35 g/cm3, powder 2 is 5 : 2 : 3 and weighs 44 g/cm3, and powder 3 is 4 : 15 : 1 and weighs 43 g/cm3. The mystery mixture is 2 : 2 : 3. The challenge is: how much of each powder is in the mixture, and how much does the mixture weigh per cm3? Answer in 1 : 2 : 3 and g/cm3.