Category: Math

Galvanizing Growth Python Simulation

import pandas as pd
from random import random
from math import floor, log
import matplotlib
from matplotlib import pyplot as plt
from numpy.random import normal
group = {}
growth = {}
countries = [('China', 137e7, 274e6), ('India', 127e7, 254e6), ('United States', 324e6, 648e5), ('Indonesia', 258e6, 516e5), ('Brazil', 206e6, 412e5), ('Pakistan', 202e6, 404e5), ('Nigeria', 186e6, 372e5), ('Bangladesh', 156e6, 312e5), ('Russia', 142e6, 284e5), ('Japan', 127e6, 254e5), ('Mexico', 123e6, 246e5), ('Philippines', 103e6, 206e5), ('Ethiopia', 102e6, 204e5), ('Vietnam', 953e5, 1906e4), ('Egypt', 947e5, 1894e4), ('Iran', 828e5, 1656e4), ('DR Congo', 813e5, 1626e4), ('Germany', 807e5, 1614e4), ('Turkey', 803e5, 1606e4), ('Thailand', 682e5, 1364e4), ('France', 668e5, 1336e4), ('United Kingdom', 644e5, 1288e4), ('Italy', 62e6, 124e5), ('Burma', 569e5, 1138e4), ('South Africa', 543e5, 1086e4), ('Tanzania', 525e5, 105e5), ('South Korea', 509e5, 1018e4), ('Spain', 486e5, 972e4), ('Colombia', 472e5, 944e4), ('Kenya', 468e5, 936e4), ('Ukraine', 442e5, 884e4), ('Argentina', 439e5, 878e4), ('Algeria', 403e5, 806e4), ('Poland', 385e5, 77e5), ('Uganda', 383e5, 766e4), ('Iraq', 381e5, 762e4), ('Sudan', 367e5, 734e4), ('Canada', 354e5, 708e4), ('Morocco', 337e5, 674e4), ('Afghanistan', 333e5, 666e4), ('Malaysia', 31e6, 62e5), ('Venezuela', 309e5, 618e4), ('Peru', 307e5, 614e4), ('Uzbekistan', 295e5, 59e5), ('Nepal', 29e6, 58e5), ('Saudi Arabia', 282e5, 564e4), ('Yemen', 274e5, 548e4), ('Ghana', 269e5, 538e4), ('Mozambique', 259e5, 518e4), ('North Korea', 251e5, 502e4)]
groupKeys = []
scale = 50
for i, j, k in countries:
  group[i] = [[0, j, 0, k]]
  growth[i] = [0]
  groupKeys.append(i)
group[groupKeys[0]] = [[13, countries[0][1]-13, 0, countries[0][2]]]
growth[groupKeys[0]] = [13]
e = 2.7183
def eDistribute(bottom, top, original):
  if(top == bottom):
    return top
  return top*e**((bottom-original)/(top-bottom))
def grow(sets, keys, past, index, spread=lambda a,b:1, expose=lambda a:1, expand=0.05, cut=5, spreadFactor=0.5, growthFactor=10):
  spreadSum = 0
  for i in keys:
    if(sets[i][index][0]+sets[i][index][1] == 0):
      adjExpand = 0
    else:
      adjExpand = expand * sets[i][index][1]/(sets[i][index][0]+sets[i][index][1])
    if(len(sets[i]) == index+1):
      sets[i].append([sets[i][index][0], sets[i][index][1], sets[i][index][2], sets[i][index][3]])
      past[i].append(0)
    for j in keys:
      if(i != j):
        currentSpread = spread(past[i], past[j])
        spreadSum -= currentSpread
        todaySpread = round(normal(1.5, 1)*eDistribute(0, spreadFactor, currentSpread)*sets[i][index][0]*expand)
        if(todaySpread > 0):
          if(len(sets[j]) == index+1):
            sets[j].append([sets[j][index][0]+todaySpread, sets[j][index][1]-todaySpread, sets[j][index][2], sets[j][index][3]])
            past[j].append(todaySpread)
          else:
            sets[j][index+1][0] += todaySpread
            sets[j][index+1][1] -= todaySpread
            if(sets[j][index+1][1] < 0):
              sets[j][index+1][0] += sets[j][index+1][1]
              sets[j][index+1][1] = 0
            past[j][index+1] += todaySpread
    currentSpread = expose(past[i])
    spreadSum -= currentSpread
    newGrowth = round(normal(1.5, 1)*eDistribute(0, growthFactor, currentSpread)*sets[i][index][0]*adjExpand)
    sets[i][index+1][0] += newGrowth
    sets[i][index+1][1] -= newGrowth
    past[i][index+1] += newGrowth
    if(sets[i][index+1][1] < 0):
      sets[i][index+1][0] += sets[i][index+1][1]
      past[i][index+1] -= sets[i][index+1][1]
      sets[i][index+1][1] = 0
    if(index >= cut):
      if(past[i][index-cut] > sets[i][index+1][0]):
        past[i][index-cut] = sets[i][index+1][0]
      sets[i][index+1][0] -= past[i][index-cut]
      sets[i][index+1][2] += past[i][index-cut]
  for one in sets:
    spreadSum += sets[one][index+1][0]
    if(sets[one][index+1][0] > sets[one][index+1][3]):
      spreadSum += 10*(sets[one][index+1][0]-sets[one][index+1][3])
  return spreadSum

impact = 0
impacts = {}
spreadFactor = 0.5
growthFactor = 1.25
meantime = 11
incperiod = 8
strictness = 100, 70
def adj(maxVal):
  def decorator(f):
    def wrapper(*args, **kwargs):
      raw = f(*args, **kwargs)
      if(raw < maxVal):
        return maxVal - raw
      return 0
    return wrapper
  return decorator
compensate = growthFactor*scale + spreadFactor*scale**2
def testAlgs(ban, close):
  i = 0
  impact = 0
  while i < 10:
    j = 0
    while i < 150:
      impacts[str(i)] = impact
      impact = floor(impact + compensate + grow(group, groupKeys, growth, i, spread=lambda a,b:ban(a, b, i-incperiod), expose = lambda a:close(a, i-incperiod), expand = 0.029, cut=meantime+incperiod, spreadFactor=spreadFactor, growthFactor=growthFactor))
      j += 1
  return impact / 10

Galvanizing Growth

This challenge on growth involves algebra, calculus, and some combinatorics.

Consider a pandemic outbreak. It begins with patient zero in a random country. For this challenge, only consider the countries with the 50 largest populations, rounded to four significant digits. Now, there are two ways the pandemic can grow. It can either expand within a country, or expand by travel to another country. There are then several methods to stop an outbreak: cutting travel, quarantining, and social distancing. The impact of a pandemic can be calculated by the net cost of these method, plus the cost of the sickness. Now, the more seriously we try to do any of these methods, the more costly and inefficient it will become. We express this with the first equation below for quarantine and social distancing, the second for travel restrictions. Now, let the expansion of a virus within a country be dictated by the third equation below, and the expansion between any two, the fourth. The cost of each case is then given by the fifth equation. The challenge is to find a general formula, given a segment of a countries net cases curve, to determine how much a country should enact social distancing, and how strictly it should quarantine victims. And another, complementary function, given curve segments for two countries, that will give the restriction on travel that the first should impose on the latter. The curves represent the data from an incubation period, x, ago, and this is randomly generated each pandemic be the sixth equation. They recover after a recovery time, y, given by the seventh. In the below equations, cn represents money spent on efforts in country n, in cost of cases in country n, pn is population, and r is random number 0 ≤ r < 1, different each time. anx gives the number of interactions between people, with an1 within a country, an2 between two. sn is the number of cases in country n, and gn is the number of new cases in that country from that country. gab is the number of new cases spread from b to a. Good luck! A python simulation of this has been published for you to test your strategy.

a_{n1}=125\ e^\frac{-c_n}{100}\\[8pt] a_{n2}=5\ e^\frac{-c}{5}\\[16pt] g_n=\left\lfloor a_{n1}s_n{\left({3-2\sqrt2\operatorname{erfc^{-1}}{(r)}\over200}\right)}\left(1-\frac{s_n}{p_n}\right)\right\rfloor\\[16pt] g_{a_b}=\left\lfloor a_{b2}s_b{\left({3-2\sqrt2\operatorname{erfc^{-1}}{(r)}\over200}\right)}\left(1-\frac{s_a}{p_a}\right)\right\rfloor\\[16pt] i_n=s_n+10\left(s_n-\frac{p_n}5+|s_n-\frac{p_n}5|\right)\\[16pt] x=5-3\sqrt2\operatorname{erfc^{-1}}{(2r)}\\[8pt] y=11-5\sqrt2\operatorname{erfc^{-1}}{(2r)}
SIMULATION
SOLUTION

Seriocomic Set

This challenge requires some knowledge of calculus and trigonometry, but mainly algebra.

We begin this challenge with a set of 4 numbers which has the following properties. Can you find them? If you can, good for you. But do you understand the use of this week’s adjective?

a,\,b,\,c,\,d\in\mathbb Z\\[8pt] a\leqslant b\leqslant c\leqslant d\\[8pt] a+b+3=a+d=\cos'{\pi}\\[8pt] \int \frac{d-c}a+1\;\;\delta a\bigg\lt\cos'{(a+b)\pi}\bigg\lt\int\frac{1-a}b-2\;\;\delta b\\[8pt] 0\lt|bc|+1\leqslant a+b+c+d\lt5\\[8pt] bc\notin\{a^2|a\in\mathbb N\}

Note: when calculating integrals, assume the ‘+c’ that you would add at the end is equal to the variable c.

SOLUTION

Radical Rectangles

This challenges covers geometry and algebra.

We have 3 rectangles, X Y and Z. Rectangle X has sides with lengths A and B. Rectangle Y, C and D, and rectangle Z, D and E. Rectangle X has the same perimeter as rectangle Y and the same area as rectangle Z. The total perimeter of the three rectangles is 46 centimetres, and the total area, 39 square centimetres. All sides have integral centimetre lengths. Find the sum A+B+C+D+E.

SOLUTION

Curious Colonies

This science challenge requires an understanding of bacterial growth.

Diagram of the Curious Colonies

You receive an internship at Joana the scientist’s bacteria laboratory. Remember Joana from Pure Water and Spring Forward? She’s studying some exquisite bacteria. No bacteria colonies can grow over others, but they just block each other’s progress. Joana is studying them on a circular dish with diameter 1 metre. Zigzag bacteria colonies’ radii increase by 4 centimetre a minute. Linear bacteria grow at 2 centimetres a minute. Checkerboard bacteria grow at 5 centimetres a minute. Dotty bacteria grow by 1 centimetre every minute, and Inscribed bacteria grow by 3 centimetres a minute. Joana wants to display the results by simultaneously starting one colony of each type on the border of the dish. After some time, all the bacteria colonies will reach an equilibrium. The challenge is to determine where to place the colonies so that they will all end with an equal portion of the dish.

Solution

Salamandriform Sea

Geometry, calculus, and angle theorems are used in this challenge.

You are going on a vacation to an island in a sea. It’s a long journey. First, you have to drive to the sea. You park your car, take off your motorboat which you carried on top of it, and embark onto the sea. Then, you take your boat up to the island, park it, and walk up to your cottage. The sea and island are both ellipses, Whose foci are co-linear and point to your starting point. The sea and island both have their major axes twice the length of their minor axes, and you are a minor sea axis away from the closest point to the sea. Driving is 3 times faster than boating, which is thrice as fast as walking. The sea has only one island, and is 8 ninths water. What is the quickest route to your cottage?

Recondite Raking

This post is not categorized in any of our standard categories. It has a little bit of everything, but not enough of anything to be considered part of that category.

Illustration of you contmplating your chore.

There is an infinite plane. It has an infinite amount of leaves. There is one ‘leaf unit’ per square metre. You are raking all of these leaves. You want to find the best way to rake the leaves; there are infinitely many, so the littlest efficiency will save you an infinite amount of time. It takes you 1 time unit to move a metre with no leaves. It takes you two time units to move a metre with 10 leaf units on your rake. 3 with 20, and so on. Your rake has length 0.5 metres. That means you can pick up a leaf 25cm to your right or left without moving to it. To bag a pile of leaf units, it takes 2 time units plus 1 for every 5 leaves. A ‘pile’ of leaves must have a radius of no more than a metre. Can you figure out the most efficient plan? How many time units per leaf unit raked?

solution

Captivating Circles BONUS

This bonus science challenge pays tribute to our old Captivating Circles series. It involves physics. You may ask, ‘will there be a Fascinating Frequencies bonus math challenge?’ Yes, 27 weeks after the last problem. Why 27? It’s about 6 months.

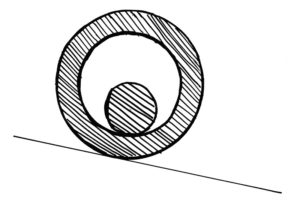
Illustration of Cylinders before they begin to roll.

In this bonus challenge, we have a cylinder. It has a smaller cylinder cut out of it. Inside this hole is an even smaller cylinder. The ratio of radii of the big cylinder to that of the hole to that of the small cylinder is 3:2:1, and the smallest one is 0.1 metres. Both the cylinders have equal density. The kinetic friction between the big cylinder and the ground is a kilogram per second. This unit seems weird because we haven’t multiplied by the velocity. That between the small and big cylinders is 5 kg/s. The ground is inclined by 10 degrees in the direction the cylinder is facing. It will begin to roll, and reach a stable speed eventually. The challenge is to figure out how fast.

solution

Loopy Lines

You will need to use geometry and algebra to solve this challenge.

Graph of Loopy Lines for this challenge.

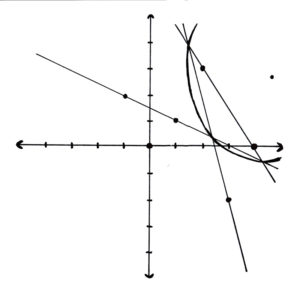
We begin this challenge with 2 points. These points are at (1, 1) and (-1, 2). You may know that it only takes 2 points to define a line. You may have guessed that that is what we will use these points for. A second line is drawn, and it passes through the point (3, -2). A third line is then drawn, and it passes through points (2, 3) and (4, 0). A circle is drawn from the 3 intersection points. The radius of the circle is 5 units. The challenge is to find it’s centre.

solution