Challenges cover a variety of topics
You will need all your skills in graph theory, and pathmaking, algebra and combinatorics to solve today’s challenge. Good luck!
This captivating circle has been divided in to many sections. By combining these sections, you can make many different composite shapes. The challenge is to see how many shapes you can make. This includes the entire circle.
Today, we have a new captivating circle, and it is the first challenge to require the use of combinatorics. It also requires some trig and pathmaking.
Our second captivating circle is a circle with 7 points on its circumference. The points are equally spaced. Each point connects to 2 others through the circle and 2 others through a straight line. No points can connect to another through both a line and arc. The circle has circumference π. How many possible different sets of connections can be made? And of these, what is the highest possible distance that must be traversed to get between 2 points?
Today we begin a special series, captivating circles. This challenge requires trigonometry and geometry.
The first captivating circles challenge is to find the area of the shaded region in the circle in the diagram. All vertices of the white triangle are on the circumference of the big circle, and the small circle is tangent to all 3 sides of the triangle. You may find that this problem requires theorems and formula’s not normally required. Do not be afraid to research the tools you need to solve this problem or other captivating circles, it’s knowing which tools to use that’s the challenge.
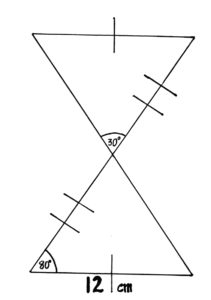
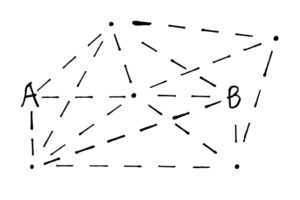
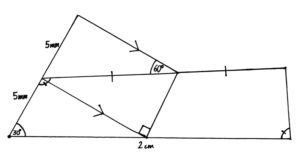
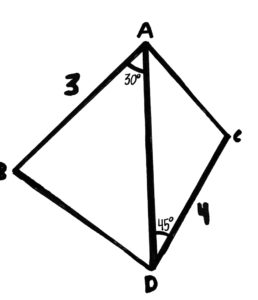
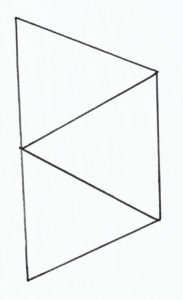
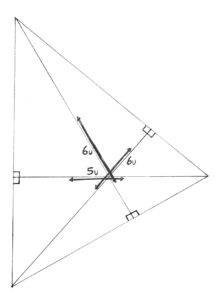
Graph theory and algebra are required to solve this challenge.
Our challenge begins with a set of points. There are points of red, orange, yellow, green, blue, and purple. These points are all interconnected as follows. Every red point connects to 1 red point, 2 orange points, and 3 green points. Each orange point connects to 1 red point, 2 orange points, 2 yellow points, and 1 blue point. All yellow points connects to 1 orange point, 1 other yellow point, 3 green points, and 1 purple point. Green points all connect to 1 red point, 4 yellow points, and 1 blue point. All of the blue points connect to 2 orange points, 3 green points, and 1 purple point. And finally, purple points connect to 4 yellow points, 1 blue point, and 1 purple point. The question is this: what is the minimum number of points for each colour?
Solving this challenge requires an understanding of geometry, trigonometry, and angle theorems.
In today’s challenge, we face two triangles who are not congruent. This is surprising because they appear identical, and we are told they share two sides. We can find that they also share and angle. However, because the angle isn’t between the sides, it’s only SSA. SSA is not a valid congruency theorem, because in some cases it gives two possible solutions. In this case, we have both of them, directly connected. The question is this: what is the length of the line that is cut unevenly? That is, the one whose length equals the sum of the sides that the triangles do not share.
In today’s challenge, you will have to use your pathmaking and graph theory skills.
The challenge is to make as many connections as you can. However, your connections must follow these rules: 1. All connections must be on a dotted line, and 2. That path must start at A and end at B.
In today’s challenge, you will need to use trigonometry, angle theorems, and geometry.
The challenge for today is to find the area of the entire figure. We are given 3 lengths, 2 angles, 1 length equality, an angle equality, and finally, 1 set of parallel lines. Remember the units!
Today’s challenge features the concepts of geometry, angle theorems, and trigonometry. No calculator required, though.
The challenge for today is to find the area of △ABD, given that the area of △ACD is √2, that AB is 3, DC is 4, ∠BAD = 30°, and ∠ADC = 45°.
In today’s challenge, you will need the concept of path-making.
In today’s challenge, we have 5 connected points. Can you find the number of possible paths, starting and ending at intersections, that never use the same intersection twice?
Todays challenge requires you to understand the pythagorean theorem, in the topic of geometry. You will also need to comprehend angle theorems.
The altitudes in a triangle measure 5, 6, and 6 units. The perimeter of said triangle is 20 units. The challenge for today is: What’s the area?