Category: Pathmaking

Crazy Capture

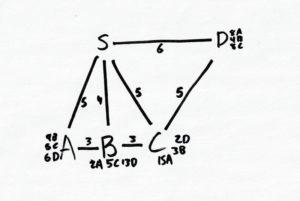
All of your algebra, geometry, trigonometry, angle theorems, and pathmaking skills are required to have a chance of solving today’s challenge.

2D capture example.

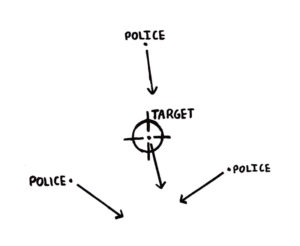
In a mathematical capture, all police officers and the target are points that travel at the same constant speed in infinite space in n dimensions. They have infinite endurance and perfect reaction time. The target is instantly captured and cannot ecape when a police officer touches it. In 1 dimension, when n = 1, it obviously takes 2 officers surrounding the target. When n = 2, we can do it with three easily. We do this by dividing the plane into three, each officer can easily trap the target in a 120° slice. The challenge is to see how many officers it takes to capture the target when n equals 3, in three dimensions.

Solution

Devising Deactivation

To solve this challenge, you will need to use geometry, trigonometry, and algebra, to do pathmaking.

Map of the radar that must be deactivated.

You are working for the government as a mathematician and they tell you of a problem. There is a plan afoot to compromise an enemy radar station. It is critical that the invading crew member is undedected, as the enemy must not know that their radar is sending them misinformation. However, the radar has a range of 100 metres and completes a rotation every 12 seconds. The fastest crew member can only sprint at 7 metres per second with their toolkit. Because of the radar’s length and rotation speed, it is nearly impossible to disable it undetected. None of the simple strategies work. The challenge is to find a path that the invader can take without being detected.

Solution

Captivating Circles 4

You will need all your skills in graph theory, and pathmaking, algebra and combinatorics to solve today’s challenge. Good luck!

Captivating Circle #4

This captivating circle has been divided in to many sections. By combining these sections, you can make many different composite shapes. The challenge is to see how many shapes you can make. This includes the entire circle.

Solution

Captivating Circles 2

Today, we have a new captivating circle, and it is the first challenge to require the use of combinatorics. It also requires some trig and pathmaking.

Captivating Circle #2

Our second captivating circle is a circle with 7 points on its circumference. The points are equally spaced. Each point connects to 2 others through the circle and 2 others through a straight line. No points can connect to another through both a line and arc. The circle has circumference π. How many possible different sets of connections can be made? And of these, what is the highest possible distance that must be traversed to get between 2 points?

Solution

Optimal Route

This diagram shows the bus stops, the distances as numbers, and the number of people going to other stops for each stop.

Today’s challenge covers the concept of optimal path-making.

Can you find the bus route that is the best for everyone? The bus driver counts too. Each big letter is a bus stop. The small letters next to the big letters represent other stops that people at the station want to go to. The numbers are the amount of people going to that stop. S it the bus depot, the start and end.

Solution