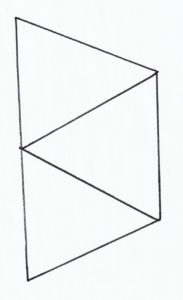
In today’s challenge, you will need the concept of path-making.
In today’s challenge, we have 5 connected points. Can you find the number of possible paths, starting and ending at intersections, that never use the same intersection twice?
Challenges cover a variety of topics

In today’s challenge, you will need the concept of path-making.
In today’s challenge, we have 5 connected points. Can you find the number of possible paths, starting and ending at intersections, that never use the same intersection twice?
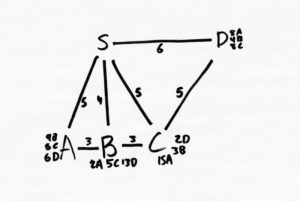
Today’s challenge covers the concept of optimal path-making.
Can you find the bus route that is the best for everyone? The bus driver counts too. Each big letter is a bus stop. The small letters next to the big letters represent other stops that people at the station want to go to. The numbers are the amount of people going to that stop. S it the bus depot, the start and end.
This challenge utilizes the concepts of basic graph theory and counting.
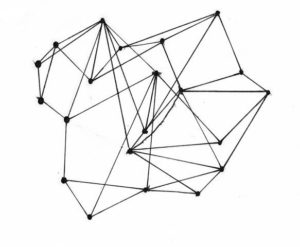
The challenge is to find the highest possible minimum number of lines needed to be traversed to get between any 2 arbitrary points.