Category: Algebra

Loopy Lines

You will need to use geometry and algebra to solve this challenge.

Graph of Loopy Lines for this challenge.

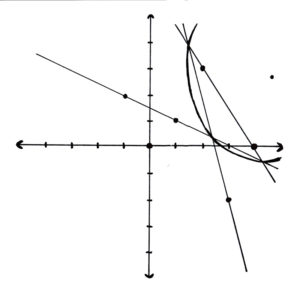
We begin this challenge with 2 points. These points are at (1, 1) and (-1, 2). You may know that it only takes 2 points to define a line. You may have guessed that that is what we will use these points for. A second line is drawn, and it passes through the point (3, -2). A third line is then drawn, and it passes through points (2, 3) and (4, 0). A circle is drawn from the 3 intersection points. The radius of the circle is 5 units. The challenge is to find it’s centre.

solution

Sophisticated Streetcar

Algebra, trigonometry, and calculus are used in today’s challenge.

You are taking a streetcar through a city. Your destination is in the middle of a large park, and you are late. You can jump of the streetcar at any time while it is on the side of the park. Your destination is 1 kilometre from the road. The streetcar moves at 15 m/s, and you move at 5 when you run, which you will to try to be on time. You calculate when you will need to jump off the streetcar to arrive as soon as possible, and jump of exactly then. For how long do you run?

Solution

Didactic Dice

Combinatorics is needed to solve today’s challenge.

Shown in the diagram to the right is the board for a dice game. The rules are as follows: start at the point. On your turn, roll 2 six sided dice. Move forward thet many spaces allong the path. The path is marked by the arrow and has 24 squares. If you reach the black square and have more moves, move back to the dot. You do not continue moving; your turn ends immediately. The first player to end exactly on the black square wins. You play this game with a friend. The challenge is to find the average number of turns the game will take. After 1 player wins, the other does not continue. This is very important.

solution

Sophisticated Shapes

In this challenge, you will need to use geometry, calculus, algebra, and angle theorems.

A roulette is a shape created by rolling things. If you roll circles, you have a trochoid. If you draw the path of a point on the circumference, you have a cycloid. And if you roll that circle inside another circle, you have a hypocycloid. Simple enough. Say you have a circle with radius 25 centimetres and a circle with radius 1 metre. When you rotate the smaller circle inside the bigger one, the path traveled by a point on the circumference is a hypocycloid. It will touch the bigger circle 4 times every rotation. At these points, the instantaneous velocity of the point is zero. The challenge is to find the instantaneous acceleration if the small circle completes 1 revolution inside the bigger one each second. This is different from rolling completely over the inside, which it will do every 4.

solution

Peculiar Products

Trigonometry, geometry, ad algebra are required to solve todays challenge.

Pi notation is to Sigma notation as plus is to minus. Sigma notation is the sum of a bunch of stuff, Pi is the product. Pi is also ≈3.1416, but we will note that as π. In Strange Sums, we evaluated an expression with 2 Sigmas. Here will will find the product of the outputs of an equation. Specifically, the equation for the area of a regular polygon. Better go find that one out right now if you don’t know it. We will express this function as A(n, s), where n is the number of sides and s the length of them. Now solve the expression below.

\prod_{k=1}^\infin\Bigg(A\bigg(k,\,\frac1{tan (90\degree)-\frac{360\degree}k}\bigg)\Bigg)
Solution

Exquisite Equation

Advanced algebra is required to solve this challenge. You should read Perplexing Protons before beginning this challenge.

We left an unsolved equation after solving Perplexing Protons. In this challenge, we will solve it. Good luck!

x=5\,000\,000+E^+\frac{2-e^ {\frac{-1}{N^+}}-e^\frac{-3}{N^+}}{N^+} +E_{t=3.25}-3E^+-1\\[8pt] \frac{E^+-E^+e^\frac{-3}{N^+}} {N^+e^\frac1{N^+}}=1\,000\,000
Solution

Strange Sums

Algebra and geometry are needed to solve this challenge.

Sigma notation is the topic of today’s challenge. At the bottom, we set a variable, usually ‘K’. K typically starts at 0 or 1. We would write ‘k=0’ or ‘k=1’ below the Sigma. Sigma notation is often used to denote the partial or full sum of an infinite series. At the top, we say when the series will end, often infinity. The value of the expression is the sum of the stuff to the right of the sigma for every value of K. The challenge for today is to find the sum of the expression. Look out for the sequel to this challenge, Peculiar Products, in which we will discuss Pi notation.

\sum_{k=2}^{\infin}\Bigg(\sum_{l=0}^{\infin} \Big(\frac1{k^l}\Big)\Bigg)
Solution

Complex Coins

You will need to use algebra and combinatorics to solve this challenge.

A normal coin has 2 flat sides and one thin round edge. When tossed, the coin always lands on a flat side. A brand new pencil has 2 small flat sides and 1 long round side. When tossed, the pencil always lands on the round side. Somewhere in the middle is the 3 sided coin, where all 3 sides are equally likely to be rolled. You happen to have 5 such 3 sided coins*. You call the 3 sides heads, tails, and round, or H, T, and R for short. You and your friend John a game with these coins. For every H, you get a point. For every T, John gets a point. But for every R, you both get a point. First to 5 points wins. You start playing, and roll 2 tails and a round. What is the probability that you win?

*Despite various lengthy efforts, nobody has been able to produce a perfect 3 sided coin as described in this challenge. So far. Some have come close, see “How thick is a three-sided coin?” from Standupmaths on Youtube, available below.

Solution