We wanted to find a way to position the colonies so that they all have the same area. It’s very interesting and fun to make cool pictures, models, and simulations of bacterial colony growth. But even just theorizing will do for this problem. The slowest colony, the Dotty bacteria colony, only grows at 1 centimetre a minute, but must still occupy 20% of the area. If the Dotty colony is with only the Linear bacteria, and opposite them, it will still fall short of 20%. Thus it is clearly impossible. You must tell Joana that the colonies cannot all start at the border and occupy equal areas. She must choose one.
Author: zachary
Curious Colonies
This science challenge requires an understanding of bacterial growth.
You receive an internship at Joana the scientist’s bacteria laboratory. Remember Joana from Pure Water and Spring Forward? She’s studying some exquisite bacteria. No bacteria colonies can grow over others, but they just block each other’s progress. Joana is studying them on a circular dish with diameter 1 metre. Zigzag bacteria colonies’ radii increase by 4 centimetre a minute. Linear bacteria grow at 2 centimetres a minute. Checkerboard bacteria grow at 5 centimetres a minute. Dotty bacteria grow by 1 centimetre every minute, and Inscribed bacteria grow by 3 centimetres a minute. Joana wants to display the results by simultaneously starting one colony of each type on the border of the dish. After some time, all the bacteria colonies will reach an equilibrium. The challenge is to determine where to place the colonies so that they will all end with an equal portion of the dish.
Salamandriform Sea
Geometry, calculus, and angle theorems are used in this challenge.
You are going on a vacation to an island in a sea. It’s a long journey. First, you have to drive to the sea. You park your car, take off your motorboat which you carried on top of it, and embark onto the sea. Then, you take your boat up to the island, park it, and walk up to your cottage. The sea and island are both ellipses, Whose foci are co-linear and point to your starting point. The sea and island both have their major axes twice the length of their minor axes, and you are a minor sea axis away from the closest point to the sea. Driving is 3 times faster than boating, which is thrice as fast as walking. The sea has only one island, and is 8 ninths water. What is the quickest route to your cottage?
Solution to Centrifuge System
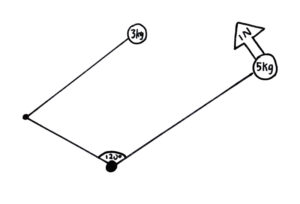
We are trying to find the rotations per minute of this system after a force of 1 newton from stationary for 1 second. It is important to note that, since the small weight is being pulled by the second pivot, it will be at a right angle to the wire connecting the two pivots. The Pythagorean theorem says that it’s distance from the centre will be 5 centimetres. This is the same as that to the first weight and force, so we do not need to consider torque. The total weight is 8 kg. A newton is just a mkg/s2. Multiply by time and divide by weight to get the total change in velocity. The angle is of no importance because we are dealing with angular momentum. 1 times 1 divided by 8 gives 0.125 metres per second. The system began stationary, so this is the new velocity. The circumference is 2πr=31.42 centimetres or ≈0.3142 metres. Divide speed (m/s) by distance (m) to get rate (r/s). Multiply by 60 to get rpm. 0.125/≈0.3142*60≈23.87 rpm. The answer is 23.87 rotations per minute.
Centrifuge System
Physics is required to solve the first part of this challenge.

The challenge begins with massless pivot anchored to the ground. Connected to the pivot by two unbending metal rods a fixed third rotation apart are a weight and another massless pivot. The weight is 5 cm from the centre, the other pivot, 3 cm. The pivot is clockwise of the weight. Attached to the second pivot, there is also another wight, attached by another unbending rod, this one of length 3 cm. The first weight weighs 5 kilograms, the second, three. A force of 1 newton is applied for 1 second to the first weight, perpendicular to the metal rod, to make the system rotate counterclockwise. The challenge is to determine how many rotations per minute it will spin at.
Solution to Recondite Raking

We’re trying to find the most efficient way to rake leaves over an infinite plane. The simple answer is to rake in a straight line. But how frequently should you bag the leaves? Well, the amount of seconds per leaf unit picked up is proportional to the number of leaves you already have. Let the number of leaf units per bag be l, and the average seconds per leaf unit, a. Your rake has a length of 0.5 metres, so you must walk 2 metres. That means the a is 2, when l is 0. This is when we bag every zero seconds. But at that point, the time required to bag them is undefined. The limit, however, as leaf units per bag decreases, is infinite. The average time spent pushing leaves per leaf unit increases by one second per 20 leaves, so the number of seconds spent pushing the leaves is dictated by the first equation below. Now, 1 bag takes 2 seconds plus 1 second per five leaf units. Divide this by the number of leaf units to get the seconds per leaf unit. Multiply the top and bottom by 5 to simplify. Separate the l to get the second equation below. The first equation is linear and increasing. The second is hyperbolic and decreasing. The total is concave up. What is it’s minimum? The minimum is the point at which the slope is zero. The derivative of the first equation is a constant twentieth. What is the derivative of 2/l? Remember, 2/l = 2l-1. The exponent rule says it’s derivative is -2l-2. At the minimum, this plus a twentieth equals zero. Solve for l to get √10. Divide by 2 and get the optimal strategy. Rake in a straight line and bag the leaves every ≈1.581 metres. It takes only ≈0.7906 seconds to bag a square metre of leaves!
a_p=2+{l\over20}\\[8pt] a_b=\frac2l+0.2\\[8pt] a=2.2+{l\over20}+\frac2l\\[16pt] {\delta\over\delta l}\bigg(\frac2l\bigg)=-2l^{-2}\\[8pt] 2l^{-2}=\frac1{20}\\[8pt] l^2=10\\[8pt] l=\sqrt{10}\approx 3.162\\[8pt] a={\sqrt{10}\over4}\approx 0.7906Recondite Raking
This post is not categorized in any of our standard categories. It has a little bit of everything, but not enough of anything to be considered part of that category.

There is an infinite plane. It has an infinite amount of leaves. There is one ‘leaf unit’ per square metre. You are raking all of these leaves. You want to find the best way to rake the leaves; there are infinitely many, so the littlest efficiency will save you an infinite amount of time. It takes you 1 time unit to move a metre with no leaves. It takes you two time units to move a metre with 10 leaf units on your rake. 3 with 20, and so on. Your rake has length 0.5 metres. That means you can pick up a leaf 25cm to your right or left without moving to it. To bag a pile of leaf units, it takes 2 time units plus 1 for every 5 leaves. A ‘pile’ of leaves must have a radius of no more than a metre. Can you figure out the most efficient plan? How many time units per leaf unit raked?
Solution to Captivating Circles BONUS
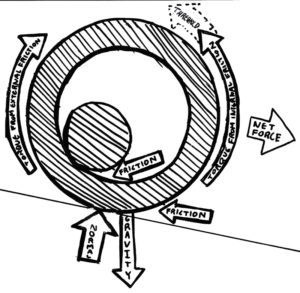
We’re trying to find the rate at which a cylinder rolls. This is actually rather simpler than you would think. For every metre the small cylinder rolls, the big one rolls three. The small one has internal friction with the big one. But, this is more than that of the big one and ground! The push of this friction is not only exerted by the big cylinder onto the small, but vice versa! Now, the cylinder would roll because of the counterclockwise torque applied by the friction with the ground. But the internal friction is so much stronger that it overpowers that torque with an even stronger clockwise torque threshold. Remember, it only happens when the counterclockwise torque is applied, so it is only a threshold. It will not cause the cylinder to roll backwards or anything crazy like that. This principle also applies to the normal force exerted by the large cylinder unto the small. Because of this, it is as if the small cylinder did not exist! Well, not really. But in a purely mathematical concept, it will be once equilibrium is reached. Knowing this, we need only look at the big cylinder. The acceleration gravity applies downward, combined with the normal force from the ground, exerts a total force dictated by the equation below. For 9.807 m/s2 and 15°, it gives 9.473 m/s2. Per metre, the kinetic friction is 1 kg/s. To equal the acceleration downwards, we divide, and get 9.473 metres per second.
\vec F_g-\vec F_n=F_g\cos\theta\\[4pt] =9.807\frac m{s^2}\times0.9659\\[4pt] =9.473\frac m{s^2}Solution to Loopy Lines
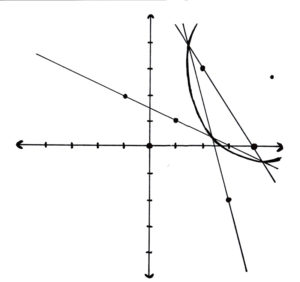
We’re trying to find the centre of a circle given the radius, a point on its circumference, and a point on a line that intersects 2 lines on its circumference. We already know one of the intersections. Since it takes 2 points to define a line, we can define 2 of the lines and find their intersection at (4.5, -0.75). Now, to find the centre of a circle, we draw the perpendiculars of 2 of the lines between the 3 points we are defining it with. Their intersection is the centre. We can use the 2 lines we know! That way, we know the slopes. Finding the intersection of 2 lines in y=mx+b form is easy peasy! x=(b1-b2)/(m2-m1), and y = m1x+b1. No problem. For the perpendiculars, we need the midpoints of the lines between intersections. No problem either, x = (x1+x2)/2, and y = (y1+y2)/2. To get a line given it’s slope and a point it passes through, we use b=y-mx. The slope is -1/m, where m was the old slope. The distance between 2 points is √((x1-x2)2+(y1+y2)2). Put all these simple things together and the answer should be easy. Let the slope of the line be x. Plugging x in through these equations gives the big equation below. A little bigger than expected. It equals 5 when x≈-2.954 and x≈-0.2364. These give the centres (5.503, 4.419), and (9.185, 0.9967).
\sqrt{\bigg(-{33x+166\over8(2x+3)}-2.053125\bigg)^2+\bigg(-{51x+214\over4(2x+3)}-{2x+3\over2x-3}-5.98125\bigg)^2}Captivating Circles BONUS
This bonus science challenge pays tribute to our old Captivating Circles series. It involves physics. You may ask, ‘will there be a Fascinating Frequencies bonus math challenge?’ Yes, 27 weeks after the last problem. Why 27? It’s about 6 months.
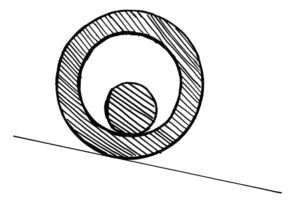
In this bonus challenge, we have a cylinder. It has a smaller cylinder cut out of it. Inside this hole is an even smaller cylinder. The ratio of radii of the big cylinder to that of the hole to that of the small cylinder is 3:2:1, and the smallest one is 0.1 metres. Both the cylinders have equal density. The kinetic friction between the big cylinder and the ground is a kilogram per second. This unit seems weird because we haven’t multiplied by the velocity. That between the small and big cylinders is 5 kg/s. The ground is inclined by 10 degrees in the direction the cylinder is facing. It will begin to roll, and reach a stable speed eventually. The challenge is to figure out how fast.
