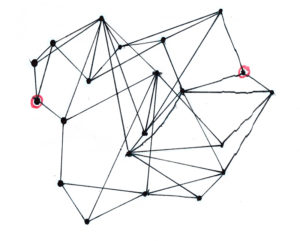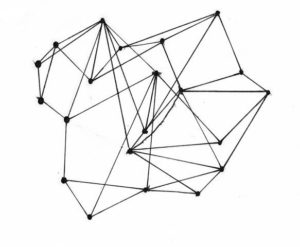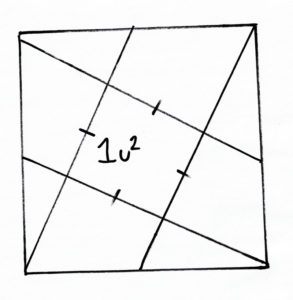
zachary – Page 16 – Zachary's Challenges

Perfect Square

You will need to understand algebra and angle theorems to do today’s challenge.

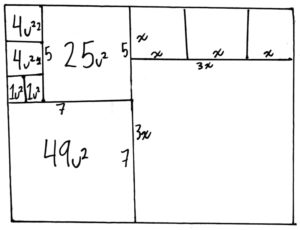
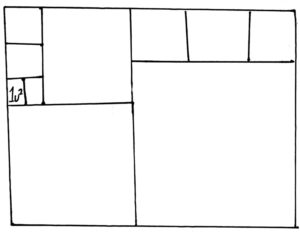
With today’s challenge, we’ll be trying to find the area of a square! All outer regions of this square have equal area, and the inner region, a square itself, has side length 1. Can you find the area of the big square? Good luck!

Solution

Solution to Divided Rectangle

In this challenge, we’re trying to find the area of a rectangle. The first square has side length 1. It shares a side with another, which must also have side 1. This makes the 2 big squares above them both have side length 2. This makes the square to the right have side length 5 units, and the one below, 7. Then we must do some algebra and find that 4x=12, x=3. This makes the very large square have side length 9, and thus the rectangle is 12 by 16. This gives it an area of 192.

Divided Rectangle

You will need algebra and geometry to solve today’s challenge.

Rectangle comprised of squares for today’s challenge.

Can you find the area of the large rectangle that encompasses all the squares, thereby solving today’s challenge? Good luck!

Solution

Solution to Shaded Square

Previously, we were trying to find the area of the non-shaded region. You will probably have found that the upper line must be parallel to the horizontal sides, and situated 2/3 of the way up the vertical ones. We know this because the steep diagonal lines clearly end 4/3 of the way across the top. This makes the slope of the steep diagonal line 1.5. The shallow diagonals must have slopes of 2/3. It follows that the lower intersections are 1/6 of the way through. This makes the lower shaded triangles both have area (1/3 * 1/2 / 2) – (1/3 * 1/6) = 1/18 each (A=B*H/2.) The upper shaded triangle clearly has base 1/2; and, height 1/3 as we showed earlier. This makes it’s area 1/12. This means the total shaded area 1/18 + 1/18 + 1/12 = 7/36, and the non-shaded, 1 – 7/36 = 29/36. The answer is therefore 29/36.

Solution

Shaded Square

In today’s challenge, you will need the concepts of geometry and trigonometry.

For today’s challenge, you must find the area of the non-shaded portion of the large square. The square has an area of 1 square unit.

Solution

Solution to Optimal Route

Diagram for bus routes in today’s problem.

We want to find the best bus route for everyone. There are many bus routes, and the only way to find the best one is via experimentation. You will thus come to the route S-D-C-B-A-B-C-D-S, which totals 1103 minutes.

Optimal Route

This diagram shows the bus stops, the distances as numbers, and the number of people going to other stops for each stop.

Today’s challenge covers the concept of optimal path-making.

Can you find the bus route that is the best for everyone? The bus driver counts too. Each big letter is a bus stop. The small letters next to the big letters represent other stops that people at the station want to go to. The numbers are the amount of people going to that stop. S it the bus depot, the start and end.

Solution

Solution to Maximum Seperation

In this challenge, we wanted to find the highest possible minimum number of lines needed to be traversed to travel between any 2 arbitrary points. For most points, this is 4. However, there are 2 for which it is 5. The answer is thus 5.