Today’s challenge utilizes the concept of algebra.
let: a+5=2-b, ab+3=a-74This time, the challenge is to see if you find all solutions to the above system of equations.
Author: zachary
Solution to Adjacent Triangles
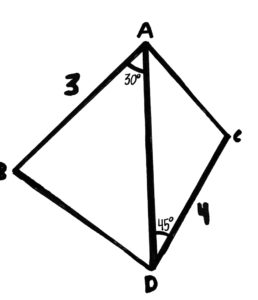
This time, we wanted to find the area of the left triangle on the left, given that the area of the one on the right has area √2. First, let’s remember that the area of any triangle, say △xyz, has area xy*yz*sin(∠xyz)*0.5. Now, we can use this formula’s inverse to find the length of ad, which will be 1. And then, we can use this to find the area of △abd, which is 0.75. ∴ the area of △abd is 0.75.
Adjacent Triangles
Today’s challenge features the concepts of geometry, angle theorems, and trigonometry. No calculator required, though.
The challenge for today is to find the area of △ABD, given that the area of △ACD is √2, that AB is 3, DC is 4, ∠BAD = 30°, and ∠ADC = 45°.
Solution to Path Counting
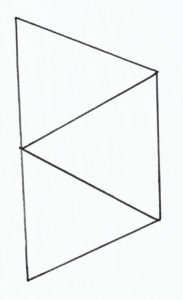
In this challenge, we wanted to find the number of paths. The easiest way to do this is by labeling the intersections, and noting the paths by the intersections. That’s because all paths start and end at intersections, and never enter the same one twice, so the paths are defined by the intersections. Now, this can be organized in anyway, like from fewest intersections to least, and then alphabetical order, or whatever. The important thing is that you dont miss any paths. Then you should get a total of 46 paths. And that’s our answer: there are 46 paths.
Path Counting
In today’s challenge, you will need the concept of path-making.
In today’s challenge, we have 5 connected points. Can you find the number of possible paths, starting and ending at intersections, that never use the same intersection twice?
Solution to Related Functions
let:f(x) = g(x+1)-x, g(x) = f(2x)-2
Now, we want to find the derivative of f( g(x) ). It is important to remember that these functions are related, entangled, if you will. With that in mind, we must not forget that derivates do not require precise functions. So. f(x) = g(x+1) – x, and that equals f(2x+2) – 2. That makes f(x) = f(2x+2) – x – 2. That means when we add x+2 to x, f(x) increases by x+2. Therefore the derivative of f(x) is 1. Now, g(x) is 2 less than twice f(x), and thus its derivative is the same as that of 2f(x). That makes g(x)’s derivative 2. Because the derivative of f( g(x) ) equals their separate derivates multiplied. That makes our answer 2.
Related Functions
You will need to understand calculus and linear algebra to solve this problem.
f(x) = g(x+1)-x,\space g(x) = f(2x)-2Today’s challenge is this: what is the derivative of f( g(x) )? Good luck!
Solution to Altitude Triangle
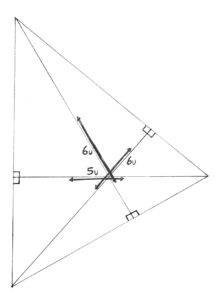
In this challenge, we’re trying to find the area of this triangle, with perimeter 20. Now, it is important to recognize that this is an isosceles triangle. That means that 2 sides are equal, and the third side is bisected. That means that if we let x and y be the side lengths, x+2y=20. Also, using the pythagorean theorem, x2 /2+25 = y2. The only solution to this is x=7.5, and y=6.25. That makes the area 5x/2, or 18.75 u2
Altitude Triangle
Todays challenge requires you to understand the pythagorean theorem, in the topic of geometry. You will also need to comprehend angle theorems.
The altitudes in a triangle measure 5, 6, and 6 units. The perimeter of said triangle is 20 units. The challenge for today is: What’s the area?
Solution to Perfect Square
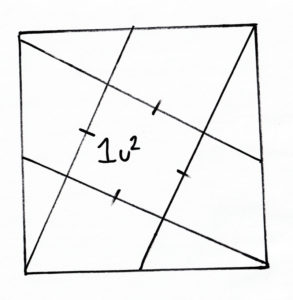
We wanted to find the area of a square! Now, the first thing we should take note of is that the small triangle is similar to the larger triangles because all of it’s angles are the same. If we let x and y be the 2 segments of the top line, x on left and y, right, then we can make an equation. specifically, find the area of the small triangle via hypotenuse comparison. The hypotenuse of the small triangle is y, and the hypotenuse of the big one is √(y2+(x+y)2). This makes y/√(y2+(x+y)2) equal one third, or (x+y)2=8y. To get this we simply raise both sides to the power of -2, subtract 1 from both sides, and then multiply by y. We also know that the area of the whole square is (x+y)^2, and that, since each outer region is a third of y(x+y), the small square is (x+y)2 – 8/3*y(x+y). That gives us the equation (x-5/3*y)*(x+y)=1. We can combine our 2 equations to solve for x and y. The positive, real number solution is x ≈ 1.120, y ≈ 0.2269, so the side of the square is ≈1.347, making it’s area 1.815 square units. And there’s our answer.