Calculus is required to solve today’s challenge.
let:f(x)=1/g(x),h(x)=-g(x)Today’s challenge is to find the antiderivative of f(x), given that the derivative of h(x) is 0.5. Remember that both functions are related to g(x).
Author: zachary
Solution to Pure Water
We wanted to know how many kilograms of hydrogen Joanne the scientist has. We know that she has 9kg of pure H₂O, no isotopes. The atomic weight of oxygen is 16, and the atomic weight of hydrogen is 1. Since there are 2 hydrogen atoms in H₂O, the ratio of hydrogen to oxygen weight is 2:16, or 1:8. This makes the hydrogen portion of total weight 1/9. Since Joanne has 9kg of water, she has exactly 1kg of hydrogen!
Pure Water
This challenge challenges your algebra skills.
Joanne is doing a science experiment. She is trying to purify water so that there are no isotopes. This means that there will be only normal H₂O molecules. If Joanne has 9kg of water after all of this, how many kilograms of hydrogen atoms does she have?
Solution to Surprising Non-Congruency
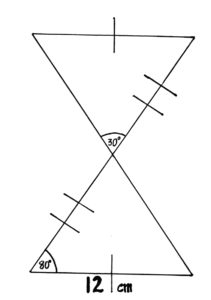
We wanted to find the length of the side which is comprised of the non-shared sides. The first thing we need to note is that, as stated in the problem, the angle opposite 30° is also 30°. We will later be able to use the law of sines to solve for the lower length. As for the angle opposite the 80°, it has to be exactly 100°. We know this because there are exactly 2 possible triangles, as mentioned in the problem, and we have both. And we can use the sine law again to find the length of the side opposite the newly-proven 100° angle. Doing this will allow us to get the answer, approximately 47.27cm.
Surprising Non-Congruency
Solving this challenge requires an understanding of geometry, trigonometry, and angle theorems.
In today’s challenge, we face two triangles who are not congruent. This is surprising because they appear identical, and we are told they share two sides. We can find that they also share and angle. However, because the angle isn’t between the sides, it’s only SSA. SSA is not a valid congruency theorem, because in some cases it gives two possible solutions. In this case, we have both of them, directly connected. The question is this: what is the length of the line that is cut unevenly? That is, the one whose length equals the sum of the sides that the triangles do not share.
Solution to Choosing Connections
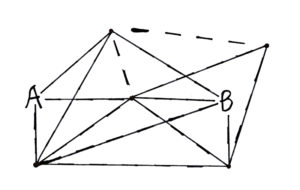
In this challenge, we wanted to find the maximum number of connections that we could add within the given conditions. Those conditions were only connecting on dotted lines, and exactly on path from A to B that goes through all other points. Note that there may be other paths from A to B, but those may not go through every point. The first step to solving this is to consider the points on the right. If we end with them, then we must come from the upper one. Then we can go to the lower. That’s because the upper one cannot reach B. If we do this, we can have an extra connection between the lower points. That one connection is needed to reach the maximum. The rest follows quickly. We are coming through the middle, so the left points must connect. We have to include the right points, so the others can all connect to B. At this point, we must remove as few outer connections as possible on the left. That would be 1, from the upper left to the centre. Now we have our final answer: 13 connections!
Choosing Connections
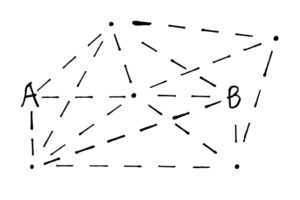
In today’s challenge, you will have to use your pathmaking and graph theory skills.
The challenge is to make as many connections as you can. However, your connections must follow these rules: 1. All connections must be on a dotted line, and 2. That path must start at A and end at B.
Solution to Parallel Pentagon
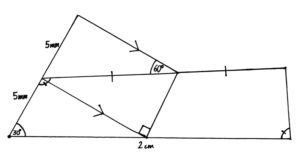
We are trying to find the area of the Pentagon this time. The first thing we can do is use the Transversal Parallel Line theorem to find that the left angle in the central triangle. Knowing that it must be 60°, we can find that the angle on the right must be 30°. We know this because the sum of the angles in a triangle is 180°. Then we can use these 2 theorems a bit more to show that all three triangles are equal. We do need to use strait angle = 180° too in some methods. Then we continue the upper parallel line to divide the pentagon into 5 triangles. We can then prove that the new ones are 30° 60° 90° too. And then all that’s left is the pythagorean theorem and area of a triangle. After all this, we have our answer: 5*(5mm * 5√3 mm / 2) = 312.5√3 mm2.
Parallel Pentagon
In today’s challenge, you will need to use trigonometry, angle theorems, and geometry.
The challenge for today is to find the area of the entire figure. We are given 3 lengths, 2 angles, 1 length equality, an angle equality, and finally, 1 set of parallel lines. Remember the units!
Solution to Equation System
let: a+5=2-b, ab+3=a-74
This time, we wanted to find the solution to this system of equations. The simplest way to do this is by using the first equation to find a in terms of b, and then substitute in the second equation. We will find that a=-b-3, and so…
-3b-b^2+3 = -b-3-74.We will find that this solves to the quadratic b^2+2b-80=0, which is equivalent to (b+10)(b-8)=0, and so has solutions b=-10 and b=8. Plug this in to our equation for a in terms of b and our solutions are as follows:
solutions: a=7,b=-10;a=-11, b=8