This is the final Captivating Circles challenge, this challenge requires the concepts of geometry and trigonometry.
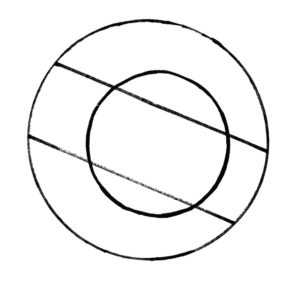
We begin this challenge with 2 concentric circles. The smaller circle divides the larger 1 into 2 equal pieces. We then draw 2 parallel chords in the large circle, which divide it evenly into three. They do not divide the small circle into three equal pieces. The challenge is then to find the area of the biggest piece in the smallest circle if the large circle has radius 1.