In this captivating circles challenge, you will need to use some algebra, some combinatorics, and some serious brainpower.
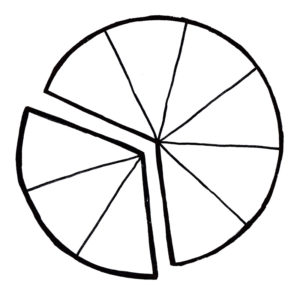
For our newest captivating circle, we are dealing with splitting oranges. The orange starts with N slices in a circle. It is then divided into 2 rings with A slices and B slices. In the diagram, N=9, A=3, and B=6. We then count one 3 and one 6. One of these rings is splitted to make 3 rings in all. We then count these rings. This continues until we can no longer split any rings as they all contain 1 slice. It happens that at the end, the number 1 is counted at least 3 more times than 2, which is counted at least 3 more times than 3, etcetera until the largest number counted. The challenge is this: what is the maximum value for N?
