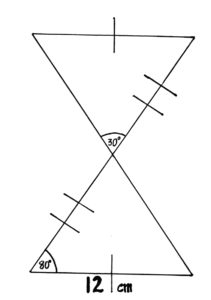
We wanted to find the length of the side which is comprised of the non-shared sides. The first thing we need to note is that, as stated in the problem, the angle opposite 30° is also 30°. We will later be able to use the law of sines to solve for the lower length. As for the angle opposite the 80°, it has to be exactly 100°. We know this because there are exactly 2 possible triangles, as mentioned in the problem, and we have both. And we can use the sine law again to find the length of the side opposite the newly-proven 100° angle. Doing this will allow us to get the answer, approximately 47.27cm.
