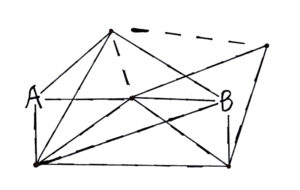
In this challenge, we wanted to find the maximum number of connections that we could add within the given conditions. Those conditions were only connecting on dotted lines, and exactly on path from A to B that goes through all other points. Note that there may be other paths from A to B, but those may not go through every point. The first step to solving this is to consider the points on the right. If we end with them, then we must come from the upper one. Then we can go to the lower. That’s because the upper one cannot reach B. If we do this, we can have an extra connection between the lower points. That one connection is needed to reach the maximum. The rest follows quickly. We are coming through the middle, so the left points must connect. We have to include the right points, so the others can all connect to B. At this point, we must remove as few outer connections as possible on the left. That would be 1, from the upper left to the centre. Now we have our final answer: 13 connections!
