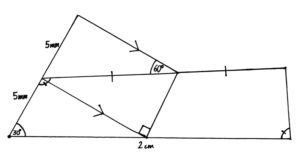
We are trying to find the area of the Pentagon this time. The first thing we can do is use the Transversal Parallel Line theorem to find that the left angle in the central triangle. Knowing that it must be 60°, we can find that the angle on the right must be 30°. We know this because the sum of the angles in a triangle is 180°. Then we can use these 2 theorems a bit more to show that all three triangles are equal. We do need to use strait angle = 180° too in some methods. Then we continue the upper parallel line to divide the pentagon into 5 triangles. We can then prove that the new ones are 30° 60° 90° too. And then all that’s left is the pythagorean theorem and area of a triangle. After all this, we have our answer: 5*(5mm * 5√3 mm / 2) = 312.5√3 mm2.
