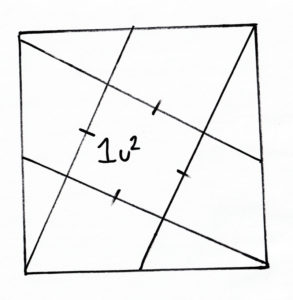
We wanted to find the area of a square! Now, the first thing we should take note of is that the small triangle is similar to the larger triangles because all of it’s angles are the same. If we let x and y be the 2 segments of the top line, x on left and y, right, then we can make an equation. specifically, find the area of the small triangle via hypotenuse comparison. The hypotenuse of the small triangle is y, and the hypotenuse of the big one is √(y2+(x+y)2). This makes y/√(y2+(x+y)2) equal one third, or (x+y)2=8y. To get this we simply raise both sides to the power of -2, subtract 1 from both sides, and then multiply by y. We also know that the area of the whole square is (x+y)^2, and that, since each outer region is a third of y(x+y), the small square is (x+y)2 – 8/3*y(x+y). That gives us the equation (x-5/3*y)*(x+y)=1. We can combine our 2 equations to solve for x and y. The positive, real number solution is x ≈ 1.120, y ≈ 0.2269, so the side of the square is ≈1.347, making it’s area 1.815 square units. And there’s our answer.
