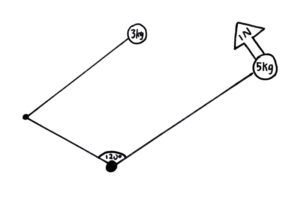
We are trying to find the rotations per minute of this system after a force of 1 newton from stationary for 1 second. It is important to note that, since the small weight is being pulled by the second pivot, it will be at a right angle to the wire connecting the two pivots. The Pythagorean theorem says that it’s distance from the centre will be 5 centimetres. This is the same as that to the first weight and force, so we do not need to consider torque. The total weight is 8 kg. A newton is just a mkg/s2. Multiply by time and divide by weight to get the total change in velocity. The angle is of no importance because we are dealing with angular momentum. 1 times 1 divided by 8 gives 0.125 metres per second. The system began stationary, so this is the new velocity. The circumference is 2πr=31.42 centimetres or ≈0.3142 metres. Divide speed (m/s) by distance (m) to get rate (r/s). Multiply by 60 to get rpm. 0.125/≈0.3142*60≈23.87 rpm. The answer is 23.87 rotations per minute.
