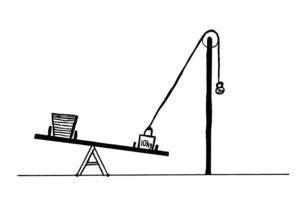
We’re trying to determine how much water must be poured into the bucket on the left to balance the balance. On the right is 2.5 metres of plank and a 10 kilogram weight. The weight is partially held up by a rope from a pulley. The weight opposite the pulley has a weight of 7 kilograms, exerting 7 kg * ≈9.807 m/s2 ≈ 68.65 mkg/s2 of tension on the rope. This lifts the 10kg weight, and so the force it exerts is equivalent to that of a 10-7 = 3 kilogram weight. It exerts a downward force of 3 kg * ≈9.807 m/s2 ≈ 29.42 mkg/s2. It is 2 metres away from the pivot, so it exerts ≈29.42 * 2 ≈ 58.84 m2kg/s2 of clockwise torque on the plank. Now, the plank on the right has a weight of 2.5 kilograms, so it exerts a downward force of 2.5 kg * ≈9.807 m/s2 ≈ 24.52 mkg/s2. It’s centre of mass is 1.25 metres away from the pivot, so it exerts a clockwise torque of ≈24.52 * 1.25 ≈ 30.65 m2kg/s2. The total clockwise torque is ≈58.84 + ≈30.65 ≈ 89.49 m2kg/s2. On the left, there is 1.5 metres of plank, weighing 1.5 kilograms. It exerts a downward force of 1.5 kg * ≈9.807 m/s2 ≈ 14.71 mkg/s2. It’s centre of mass is 0.75 metres to the left of the pivot, so it exerts a counterclockwise torque of ≈14.71 * 0.75 ≈ 11.03 m2kg/s2. Finally, water at 20° celsius has a density of 998.2 kg/m3. The bucket is 2 metres to the left of the pivot. The counterclockwise torque the water must create is ≈89.49 – ≈11.03 ≈ 78.46 m2kg/s2. This requires a downward force of ≈78.46 / 2 ≈ 39.23 mkg/s2. The mass required to exert this force is ≈39.23 / ≈9.807 ≈ 4 kg. The volume of water that has this mass is 4 / 998.2 = 4.007 × 10-3 m3. We have our answer. There is an easier way to do this problem, where we do not calculate gravity. This works because all the pieces that we start and end with do not use gravity. It makes sense because a scale would still work on the moon.
