A physics simulation is needed to solve this challenge.
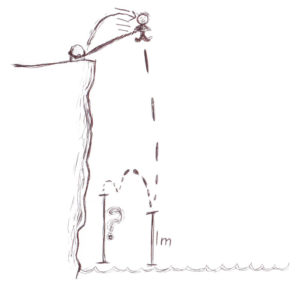
Bob the Bungee jumper from Baffling Bungee is upset about his bungee jumping experience. If you attempt the problem, you will soon see that Bob’s bungee jump will take too long. Far too long. This is because C5H8 is very springy. In fact, Bob’s bungee jump would take about 2 months … if you were thinking of a mathematical model. You see, the diagram shows a cliff behind Bob. The rubber is so springy he would bash into it, cutting his jump short. But set that problem aside for now. This challenge does not concern those. In bob’s jumps, the ups and downs would gradually, very gradually, become smaller and smaller. But they would still occur at the same frequency. Can you guess today’s challenge? Calculate that frequency.