We wanted to find the standings and satisfaction of Brutus and Craw’s vote. Brutus will vote Red, Orange, Yellow, Purple, Blue, Green. Then Craw moves his extremes to the middle to vote Blue, Purple, Green, Red, Yellow, Orange. Now Brutus moves his extremes to the middle to get Orange, Yellow, Red, Green, Purple, Blue. It will never end! Serves them right.
Table \space of \space votes\\[8pt] \begin{matrix} &\#1&\#2&\#3&\#4&\#5&\#6\\ B_1&R&O&Y&P&B&G\\ C_1&B&G&P&R&Y&O\\ B_2&Y&R&O&G&P&B\\ C_1&G&P&B&O&R&Y\\ \end{matrix}Month: August 2019
Vile Voting
Algebra and combinatorics are needed to solve this challenge.
Brutus and Craw are voting over their preference of colours. Their satisfaction is measured by how close their preferences are to the ones agreed on; they do not care about each other. The vote is determined by each player prioritizing the colours of the rainbow. Brutus and Craw do not know about indigo. Their first pick gets 5 points, their second 4, and so on such that their last gets 0.The colour with the most is first, the second most, second, and so on. Brutus and craw receive “points” of satisfaction, based on how close the vote is to their personal preferences. For each preference the number of points starts at one less than the previous, with 5 for 1st. It goes down by 2 if it’s below it’s position, and then decreases by one until it stops at 0. Except for fifth position, which cannot drop 2 because it started at only 1. In case of a tie, the position that comes first is picked randomly. First, Brutus states his preferences: red, orange, yellow, purple, blue, green. Then Craw would states his: purple, blue, green, yellow, orange, red. Except that Craw is a meanie and adjusts his to make it unfair. But Brutus then adjusts his, and they go back and forth until neither can improve their score. The challenge is to figure out what the votes, standings, and satisfaction will be for Brutus and Craw will be when they finish, if they ever do.
Satisfaction\\[16pt] \begin{matrix} & 1st & 2nd & 3rd & 4th & 5th & 6th\\ \#1 & 5 & 3 & 2 & 1 & 0 & 0\\ \#2 & 4 & 4 & 2 & 1 & 0 & 0\\ \#3 & 3 & 3 & 3 & 1 & 0 & 0\\ \#4 & 2 & 2 & 2 & 2 & 0 & 0\\ \#5 & 1 & 1 & 1 & 1 & 1 & 0\\ \#6 & 0 & 0 & 0 & 0 & 0 & 0\\ \end{matrix}Solution to Fathomless Fraction
We wanted to figure out the value of the fathomless fraction. We can start by saying the value of this fraction equals x1. x1 = 1 + 1 / x2, and so on. We can define this a recursive sequence, where xn = n + 1 / xn+1. But this doesn’t help if we don’t know any of the later terms. It approaches infinity, of course. xn>n, but xn<n+1. Maybe we could figure out the value of a term based on the previous one? xn-1 = n-1 + 1 / xn. Subtract n-1 from both sides. xn-1 -n +1 = 1 / xn. Take the reciprocal of both sides to find that xn = 1 / xn-1-n+1. We can make an alternate version of the fathomless fraction, call it fathomless equivalent fraction, or FEF for short. We soon realize that both lead to the exact same fraction. But x1 = x-1+1, and so xn=x-n+1, and we can make another fraction. But it returns to x1! It’s like with √x+1, it cannot be simplified. The answer is simply ≈1.433.
x_1=1+\frac1{2+\frac1{3+\frac1{4+…}}}\\[16pt] x_n=n+\frac1{x_{n+1}}\\[16pt] x_n=\frac1{x_{n-1}-n+1}\\[16pt] x_1=\frac1{\frac1{1+x_{-1}}}\\[16pt] x_n=x_{-n}+n\\[16pt] x_1=1+\frac1{2-2+\frac1{x_1-1}}=x_1\\[16pt] x_1 \approx 1.433Solution to Baffling Bungee
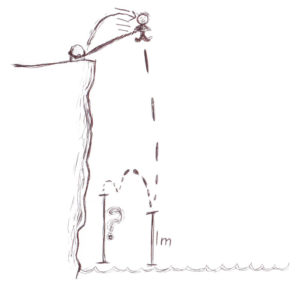
So, we’re trying to find Bob’s final height after his bungee jump. The spring constant of C5H8, normal rubber, is ≈88. The equation for the force is 1/2 kx2, where k is the spring constant and x is the portion of the natural length. When Bob begins his jump, the rubber is inactive. It’s length is zero. Thus the force of it’s pull is ≈88*02. But gravity pulls down with a force of ≈9.807 m/s2. After this we cannot continue. The simplest way is to code. Simulate the bungee jump in many microscopic steps. Calculate the pull of the elastic at each point. This will show where the lowest point of the jump is. The stable point is easily calculated. 44x2≈9.807. x2≈9.807 / 44 ≈ 0.2229. x ≈ 0.4721. The bottom of the jump is a whopping 101.7 metres down, making the answer ≈102.3 metres above the water.
PE=\frac{kx^2}2\\[16pt] 44x^2=9.807\\ x=0.4721\\[16pt] h_f=\Delta x+\approx0.5279m\\ \quad h_f=h_i-\approx0.4721m\because h_i=\Delta x+1m\\ \Delta x=101.7m\\ \Rightarrow h_i=101.7m+1m\\ \therefore h_f=101.7m+0.5279m=102.3m