We want to find the optimal strategy for renewing a book at the Leibniz Library. First, let’s look at the maximum number of days you can keep a book before renewing it. 8 at first, then 7, 7, 6, and then 4. And that’s it, you cannot renew the book again. The fine equation will start above 0 when you renew the book a fifth time. But the hold equation will max out at 100% after only 10 days. The best is clearly 16 days. But it’s very likely it will be put on hold and you’ll be stuck with 14, or worse, 8. After 2 days, the hold equation ≈22%, and the loss would be 1 day if you don’t know. But if you don’t renew, you will probably gain a day. So don’t renew then. But on day 3, you can lose 2 days, and the hold equation now ≈24%. It’s less than 33%, so the day gained would still be worth it. On day 4, the hold equation is now at ≈29%, more than 25%, so you renew. We start again on day 5, with ≈40%, it’s less than 50%, so we don’t renew. But on day 6, we have ≈51%, far more than 33%. Although we lose the possibility of an extra day, it’s quite unlikely, and not nearly enough to make it worth not renewing. So we ought to renew. Not until day 8 can we gain another day. By then the hold equation is already ≈79%. It doesn’t matter if it has been renewed yet, if it hasn’t yet we do. By the time we can gain another day, the hold equation will have reached 100%. So our answer is to renew on days 4, 6, and 8.
f(x)=d^2+5d-7cos(r)+r^3-100\\[10pt] h(x)=\frac{t^2+3sin(t)+15}{100}Day: July 28, 2019
Solution to Spinning Stick
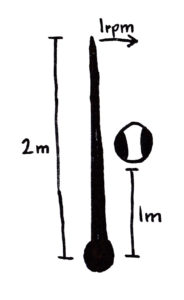
We wanted to find the velocity of the ball when it rolls off of the spinning stick. The velocity of a point stick will be 2π metres per minute times it’s distance from the origin, in whatever direction it’s traveling in. This is 90° clockwise of the direction of the stick. This vector makes a circle with radius 2π metres, and it completes a rotation at the same speed. Knowing this, we find the centripetal force the stick experiences to be 4π2 metres per minute squared multiplied by the distance, another 90° clockwise of the stick. This makes centripetal force towards the origin, as you probably already know. If to spin in a circle the ball must accelerate, then it wont. The stick does not hold it in, and so it will quickly fly away. Since acceleration is proportional to distance, velocity increases acceleration. If you try solving Captivating Circles 5, you will see that such relationships relate to e. The rotation doesn’t interfere at all, though you’d think it would. When you have they are the same size and the proportions of change equal, their sum increases exponentially. Every unit of time when one would double the other if the other wasn’t returning the favour, they both multiply by e. They multiply at the same rate even if they aren’t the same size. The difference will decrease by a factor of e in the same duration of time. If one increases the other faster by a factor of n, the other will approach being larger by a factor of √n. The distance from the correct ratio will also decrease by a factor of e in the same duration of time as before. Using this knowledge, we can calculate the velocity, using the duration of time shown before as the unit for time, and take it’s derivative to get distance. Solve this equation to equal 2, and we find the time when the ball leaves the stick. Put time back into the equation for velocity, and we have our answer. 12.3134 metres per minute.
\frac d{dx}\frac{e^t-e^{-t}}{2\sqrt{2\pi}}=\frac{e^t+e^{-t}}{2\sqrt{2\pi}}\\[16pt] t=log(2\sqrt{2\pi}+\sqrt{8π-1})\approx2.295\\[16pt] \overrightarrow v\approx\frac{e^{2.295}-e^{-2.295}}{2\sqrt{2\pi}}\approx12.313