Month: May 2019

Solution to Absurd Algebra

The Absurd Algebraic graph.

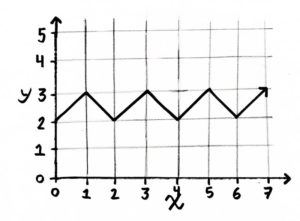
We want to find an equation representing the equation on the left. We can begin with the operator modulo, represented by %. a%b gives the remainder when you divide a by b. For example, 7%3=1. x%1 – x%2 will give us -1 when x rounds down to an event number and 0 when it doesn’t. Add 0.5 and multiply by twice x%1 to get disconnected ups and downs centered at 0. If we add (x%1 – x%2) * -1 to this, we move up only the negatively sloped lines and get a zig-zag with peaks at 0 and 1. Add 2 to get our answer, the equation below.

y=2(x\%1-x\%2+0.5)(x\%1-0.5)+2.5

Absurd Algebra

Extreme algebra knowledge and skills are required to solve this challenge.

Absurd Algebraic Graph.

This time, we are faced with a strange graph. When x rounds down to an even number, the slope is 1. But when it rounds down to an odd number, the slope is -1. This makes an intriguing zig-zag pattern with peaks always at 2 or 3. But what equation could possibly give such a line? Well, that is the challenge.

Solution

Solution to Crazy Quadrilateral

The Crazy Quadrilateral!

We wanted to find ∠FEG in the crazy quadrilateral. Since ΔABC ~ ΔADE ~ ΔHAG, we know that ∠ABC = ∠ADE = ∠HAG = 90°. This means ∠BAC = 30°. We know that ΔAGE is isosceles. It is obviously impossible to have ∠EAG equal ∠AEG. It is also impossible for ∠EAG to equal ∠AGE, because then EF would intersect AH. Thus, ∠AGE = ∠AEG, so they must both measure 75°. ∠FEG = ∠AEF – ∠AEG, so we have our answer. ∠FEG measures 15°.

Crazy Quadrilateral

You will need to use geometry, angle theorems, trigonometry, and your brain to solve this challenge.

Crazy Quadrilateral

We begin with a quadrilateral AEGH. We then draw a line from A to G to make ΔAEG and ΔAGH. ΔAEG is an isoscelese triangle. Next, we draw a line from point E to a new point, F, such that ∠AEF measures 60°. This makes a new point, D, where AG intersects FE. After that, we draw a line HC so that it is parallel to FE and intersects AG at point C. This makes ΔABC ~ ΔADE ~ ΔHAG. The challenge is to find ∠FEG if ∠HAG measures 90°.

Solution

Solution to Captivating Circles 6

Captivating Circle #6

We wanted to find the area of the largest piece of the small circle. The radius of the small circle is √2 / 2. To find the distance between 1 chord dividing the small circle and it’s centre, we use the equation below. This gives us 0.2649 units. The pythagorean theorem gives us the length of half the part of the chord in the small circle, in the second equation. This gives us 0.4298. asin(0.4298 / (√2 / 2) ) gives us half the section angle, making the section of the small circle encompassing the missing segment equal to 74.8653°. The triangle making the difference between the segment and sector has area 0.4298 * 0.2649 = 0.1139. The sector has area 74.8653π / 720 = 0.3267. π/2 – 0.3267 * 2 = 0.917. And there we have it: the area of the biggest piece in the smallest circle has area 0.9174 units squared

1-\int_{-\sqrt{h(2-h)}}^{\sqrt{h(2-h)}}\sqrt{1-x^2}\,dx – 2(1-h)\sqrt{h(2-h)}=\frac{\pi}{3}\\[16pt] x=\sqrt{(\sqrt{2}/2)^2-0.2649^2}=0.4298