Challenges cover a variety of topics
This is the final Captivating Circles challenge, this challenge requires the concepts of geometry and trigonometry.
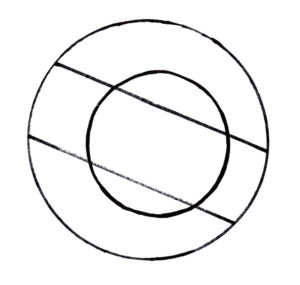
We begin this challenge with 2 concentric circles. The smaller circle divides the larger 1 into 2 equal pieces. We then draw 2 parallel chords in the large circle, which divide it evenly into three. They do not divide the small circle into three equal pieces. The challenge is then to find the area of the biggest piece in the smallest circle if the large circle has radius 1.
We can simulate the decrease in size for Jack and Jill with the javascript below:
We will find Jill’s size area to be 6.333 in the console. Divide by π and square root to get Jill’s radius after facing Jack: 1.42.
You will need to use algebra to solve this challenge. Some programming would be extremely useful as well.
In the video-game “Battle of the Blobs”*, a blob is a circular creature that deals damage over time proportional to its current area. A blob’s area will shrink proportionally to damage dealt to it. The damage over time is not dealt at short intervals, rather is always being dealt, but with the same rate. Our challenge begins when 2 blobs, Jack and Jill, battle each other. The radius of Jack is 1, and the radius of Jill is 1.5. Clearly, Jill will kill Jack. The question is what will be Jill’s radius after fighting Jack, assuming the only change in a blob’s size is caused by damage from the other.
*”Battle of the Blobs” is not a real video-game.
This challenge is extremely long. The reason for this is that there was a slight error in the drawing of the diagram. 1 line was misplaced. Apologies for the inconvenience. The diagram, when simplified to a graph, should have been rotationally symmetric. As it is, it is just barely not. because of this, the number of shapes is many times greater than it should have been. The solution to the challenge as it is will be posted nevertheless. We can label each section with letters A to L. We can then list the shapes by the sections they contain, like AB, CDG, and so on. All in all, there are 2037 shapes.
You will need all your skills in graph theory, and pathmaking, algebra and combinatorics to solve today’s challenge. Good luck!
This captivating circle has been divided in to many sections. By combining these sections, you can make many different composite shapes. The challenge is to see how many shapes you can make. This includes the entire circle.
We wanted to find the maximum number of slices for our circle. This can be done by finding an equation for the count you have an need to see where they intercept, which requires comlex factorials, making it difficult to solve. The solution is 5. We can also use trial and error to obtain this. The equations will be posted seperately.