Challenges cover a variety of topics
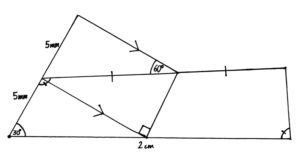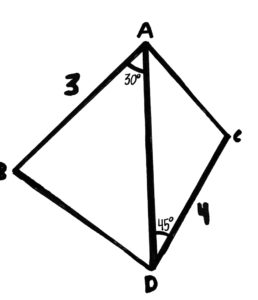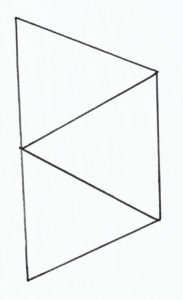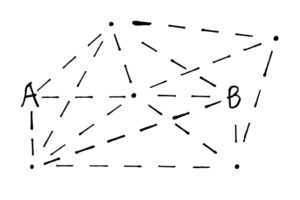
In today’s challenge, you will have to use your pathmaking and graph theory skills.
The challenge is to make as many connections as you can. However, your connections must follow these rules: 1. All connections must be on a dotted line, and 2. That path must start at A and end at B.
We are trying to find the area of the Pentagon this time. The first thing we can do is use the Transversal Parallel Line theorem to find that the left angle in the central triangle. Knowing that it must be 60°, we can find that the angle on the right must be 30°. We know this because the sum of the angles in a triangle is 180°. Then we can use these 2 theorems a bit more to show that all three triangles are equal. We do need to use strait angle = 180° too in some methods. Then we continue the upper parallel line to divide the pentagon into 5 triangles. We can then prove that the new ones are 30° 60° 90° too. And then all that’s left is the pythagorean theorem and area of a triangle. After all this, we have our answer: 5*(5mm * 5√3 mm / 2) = 312.5√3 mm2.
In today’s challenge, you will need to use trigonometry, angle theorems, and geometry.
The challenge for today is to find the area of the entire figure. We are given 3 lengths, 2 angles, 1 length equality, an angle equality, and finally, 1 set of parallel lines. Remember the units!
This time, we wanted to find the solution to this system of equations. The simplest way to do this is by using the first equation to find a in terms of b, and then substitute in the second equation. We will find that a=-b-3, and so…
-3b-b^2+3 = -b-3-74.We will find that this solves to the quadratic b^2+2b-80=0, which is equivalent to (b+10)(b-8)=0, and so has solutions b=-10 and b=8. Plug this in to our equation for a in terms of b and our solutions are as follows:
solutions: a=7,b=-10;a=-11, b=8Today’s challenge utilizes the concept of algebra.
let: a+5=2-b, ab+3=a-74This time, the challenge is to see if you find all solutions to the above system of equations.
This time, we wanted to find the area of the left triangle on the left, given that the area of the one on the right has area √2. First, let’s remember that the area of any triangle, say △xyz, has area xy*yz*sin(∠xyz)*0.5. Now, we can use this formula’s inverse to find the length of ad, which will be 1. And then, we can use this to find the area of △abd, which is 0.75. ∴ the area of △abd is 0.75.
Today’s challenge features the concepts of geometry, angle theorems, and trigonometry. No calculator required, though.
The challenge for today is to find the area of △ABD, given that the area of △ACD is √2, that AB is 3, DC is 4, ∠BAD = 30°, and ∠ADC = 45°.
In this challenge, we wanted to find the number of paths. The easiest way to do this is by labeling the intersections, and noting the paths by the intersections. That’s because all paths start and end at intersections, and never enter the same one twice, so the paths are defined by the intersections. Now, this can be organized in anyway, like from fewest intersections to least, and then alphabetical order, or whatever. The important thing is that you dont miss any paths. Then you should get a total of 46 paths. And that’s our answer: there are 46 paths.
In today’s challenge, you will need the concept of path-making.
In today’s challenge, we have 5 connected points. Can you find the number of possible paths, starting and ending at intersections, that never use the same intersection twice?
Now, we want to find the derivative of f( g(x) ). It is important to remember that these functions are related, entangled, if you will. With that in mind, we must not forget that derivates do not require precise functions. So. f(x) = g(x+1) – x, and that equals f(2x+2) – 2. That makes f(x) = f(2x+2) – x – 2. That means when we add x+2 to x, f(x) increases by x+2. Therefore the derivative of f(x) is 1. Now, g(x) is 2 less than twice f(x), and thus its derivative is the same as that of 2f(x). That makes g(x)’s derivative 2. Because the derivative of f( g(x) ) equals their separate derivates multiplied. That makes our answer 2.