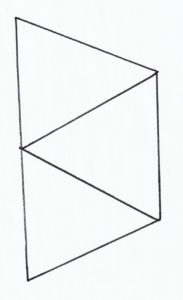
In this challenge, we wanted to find the number of paths. The easiest way to do this is by labeling the intersections, and noting the paths by the intersections. That’s because all paths start and end at intersections, and never enter the same one twice, so the paths are defined by the intersections. Now, this can be organized in anyway, like from fewest intersections to least, and then alphabetical order, or whatever. The important thing is that you dont miss any paths. Then you should get a total of 46 paths. And that’s our answer: there are 46 paths.
